Nombre de racines d'un polynôme

par **samoufar** » 12 Aoû 2017, 15:28

Ça marche

On peut aussi le rédiger sans récurrence :

• Si

est pair, alors

admet un minimum (facile à montrer), disons en

. Alors

et

(car

) Dès lors,

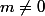
car

est pair.
Ainsi

est strictement positive, et en particulier ne s'annule jamais.

• Si

est impair, alors

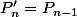
est strictement positive d'après le point précédent. Ainsi

est strictement croissante, donc l'équation

admet une unique solution réelle d'après le théorème des valeurs intermédiaires.

par **Paul1908** » 12 Aoû 2017, 15:30

Cela m'aide beaucoup !!
Merci beaucoup pour toutes vos réponses, je n'aurais pas réussi sans vous !