Suite impaire symbolique de Collatz

[samoufar]

@syrac :
Mon objectif avec ce post n'est pas d'attaquer ; je veux seulement que tu comprennes que ça ne montre rien. Effectivement, si tu campes sur ta position, ce serait une perte de temps d'y répondre...

(Et vu que c'est le cas depuis presque deux ans, je doute que ça change, cf. https://www.maths-forum.com/cafe-mathematique/collatz-les-puissances-t169343.html)

Une question : est-ce que tu as testé ta fonction sur tous les entiers qui existent ? Si oui, alors chapeau, tu viens de démontrer la conjecture, bravo (et en prime tu viens de montrer que l'ensemble des entiers est fini...) ! Si non (et c'est le cas...), tu n'as rien montré...

Au passage, c'est sympa de faire un programme pour voir ce que ça donne, mais le résultat obtenu reste une conjecture. Et non une preuve.

[syrac]

Je vais quand même répondre à ce passage :

Et pour toi, 1/2+3/4+3/4, ça n'est pas entier ? Et 1/2+3/2 non plus ? La preuve que c'est faux, quand tu prends une "suite impaire à 7 termes", l'expression de n5 ne change pas

A mon avis tu le fais exprès. Bien sûr que dans les exemples que tu cites la somme des fractions est entière ! Mais dans le contexte de mon document on a affaire à des fractions du type 1/2^a + 3/2^b + 9/2^c + 27/2^d +..., ce qui est entièrement différent puisqu'on ne connaît pas les valeurs de a, b, c, d, ... !

On sait seulement que 1/2^a ne sera jamais entier puisque la valeur minimale de a est 1, ce qui fait que la valeur maximale de la fraction sera 0,5, non entière. Peux-tu me donner un exemple de somme entière différente de 1 sur la base de 1/2^a + 3/2^b + 9/2^c + 27/2^d ? Bon courage !

Une question : est-ce que tu as testé ta fonction sur tous les entiers qui existent ?

Tu la programmes et tu donnes à n0 toutes les valeurs possibles impaires. A dans 3000 ans !

C'est ça l'avantage de la théorie, on n'a pas besoin de tester tous les nombres. Quand tu demandes à ta calculatrice de te donner la racine carrée d'un nombre, tu ne commences pas par lui demander si elle a testé son algorithme sur tous les nombres !

[syrac]

@samoufar

Je reviens sur cette histoire de fraction en prenant l'exemple de n0 = 29, parce que je veux malgré ton attitude agressive m'assurer que tu as bien compris.

suite impaire :
29, 11, 17, 13, 5, 1
exposant de 2 de ses diviseurs :
3, 1, 2, 3, 4

En effet, 3x29+1 = 88 est divisible par 2^3, 3x11+1 = 34 est divisible par 2^1, 3x17+1 = 52 est divisible par 2^2, etc. jusqu'à 5.

On fait la somme cumulée des exposants en partant de la fin, ce qui donne : 4, 7, 9, 10, 13. La valeur du dernier terme de la suite impaire de 29 est donc

n5 = 1/2^4 + 3/2^7 + 9/2^9 + 27/2^10 + 81 (3x29+1)/2^13 = quoi ? Mais 1 bien sûr !

Tu peux essayer avec autant de valeurs impaires de n0 que tu voudras, tu trouveras toujours 1.

Capito ?

[aviateur]

Bonsoir
Merci @Camouflar pour cette lecture attentive du texte et des efforts que tu as fait pour analyser le sujet.

@Syrac tu as le droit de croire en ce que tu fais et de ne pas accepter la contradiction. Néanmoins nous sommes sur un forum d'aide et pour l'image de ce forum je propose qu'il vaut mieux en arrêter là.
Cordialement.

[samoufar]

@syrac :

On sait seulement que 1/2^a ne sera jamais entier puisque la valeur minimale de a est 1, ce qui fait que la valeur maximale de la fraction sera 0,5, non entière. Peux-tu me donner un exemple de somme entière différente de 1 sur la base de 1/2^a + 3/2^b + 9/2^c + 27/2^d ? Bon courage !

Je n'ai jamais dit que c'était faux... Mon exemple vise simplement à te montrer que tu n'utilises pas les bons arguments pour le montrer. Je te retourne la question : Peux-tu me montrer qu'il n'en existe pas ? Bon courage !

Et au passage, tu prends a = b = 1 et c = d = 0 et tu obtiens ce que tu voulais.

Tu la programmes et tu donnes à n0 toutes les valeurs possibles impaires. A dans 3000 ans !

3000 ans ? Tu es très optimiste...

Quand tu demandes à ta calculatrice de te donner la racine carrée d'un nombre, tu ne commences pas par lui demander si elle a testé son algorithme sur tous les nombres !

Ça n'a pas de rapport avec le problème. Ici la question est de savoir si la conjecture de Collatz marche peu importe le premier terme de la suite. Ce que tu fais avec ton algorithme, c'est de l'extrapolation. Tu dis que ça marche jusqu'à un certain nombre (certes très grand), et tu en conclus que ça marche pour tout nombre.

Tu peux essayer avec autant de valeurs impaires de n0 que tu voudras, tu trouveras toujours 1.

Je pense que tu ne vois pas où je veux en venir... Justement, l'idée est de savoir si ce "dernier terme" existe forcément, peu importe la valeur de . A priori, rien ne te dit avec certitude que la valeur 1 va apparaître dans ta suite ; c'est l'objet même de la conjecture de Collatz.

Après, bien-sûr, si tu prends un nombre de ta liste 7, 29, 61, 117, 241, 245, 267, 483, 469, 535, 537, 965, 981, 985, il est parfaitement normal que le 6ème terme de ta suite impaire vaille 1, puisque d'une part, c'est une propriété de ces valeurs initiales, et d'autre part, tu utilises une écriture explicite de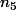 (qui, au passage, n'est pas très pratique car elle fait intervenir de nouvelles inconnues 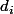). Par contre, une chose intéressante dans l'optique de ce que tu fais serait de voir si ces nombres ont une propriété particulière, et le cas échéant d'extrapoler à une suite impaire à k termes.


Encore une fois, je ne cherche pas à t'attaquer, ni quoi que ce soit de la sorte. Je souhaite simplement que tu comprennes qu'il y a quelque chose qui ne va pas, tout simplement. La critique, j'y ai souvent eu droit aussi, et franchement, c'est toujours constructif.

@aviateur : Pas de problème. Par contre ça serait sympa d'éviter d'écorcher mon pseudo

[syrac]

Ici la question est de savoir si la conjecture de Collatz marche peu importe le premier terme de la suite. Ce que tu fais avec ton algorithme, c'est de l'extrapolation. Tu dis que ça marche jusqu'à un certain nombre (certes très grand), et tu en conclus que ça marche pour tout nombre.

Si tu regardes bien, tu utilises tous les jours des formules et des algorithmes qui n'ont jamais été testés sur tous les entiers, et pour cause, c'est impossible ! Même le super-calculateur le plus puissant du monde ne le pourrait pas. Et que dire des Anciens, qui n'avaient qu'une plume et un bout de parchemin pour vérifier leurs trouvailles, celles-là même qui aujourd'hui forment le socle des mathématiques !

La forme symbolique du dernier terme d'une suite de Collatz est ce qu'elle est. Il n'y aucun empirisme là-dedans, elle décrit comment le dernier terme est formé à partir des diviseurs de la suite, et elle montre qu'il est toujours égal à 1. Si tu contestes ce résultat, alors tu peux aussi bien contester chacun des outils mathématiques que tu utilises.

A priori, rien ne te dit avec certitude que la valeur 1 va apparaître dans ta suite ; c'est l'objet même de la conjecture de Collatz.

Si, quelque chose me le dit : la forme symbolique du dernier terme, qui est incontestable.

Il y a une chose qui serait plus constructive que ce pinaillage : trouver par quel mécanisme l'expression du dernier terme aboutit à cette égalité de la somme au numérateur et du produit des diviseurs. Une fois que ce mécanisme aura été trouvé, alors on pourra dire que la conjecture est démontrée. Autrement dit, comment ce quotient de 1 apparaît-il ? C'est ça la vraie question, le cœur du problème.

[Lostounet]

Néanmoins nous sommes sur un forum d'aide et pour l'image de ce forum je propose qu'il vaut mieux en arrêter là.
Cordialement.

Je pense qu'on en arrive à un stade de saturation.

Maths-forum souffre déjà de problèmes de gestion. On a trop longtemps supporté sur ce forum les spéculations de Syrac et les pseudo-mathématiques de Arbre. Le forum n'a plus à être un lieu de débats stériles, à fond non mathématique. Toute personne qui a fait un tant soit peu de mathématiques dans sa vie semble savoir des choses qui vous échappent complètement: le principe de la démonstration et de la logique.

Donc je répète, et cela pour la dernière fois: soit on fait des mathématiques (avec tout son formalisme, sa difficulté et sa pédagogie), soit on n'en fait pas (et dans ce cas on ne reste pas).

Considérez ceci comme un dernier avertissement, Syrac et Arbre, avant un bannissement permanent de vos pseudos. Si vous souhaitez rester, ce sera pour faire des mathématiques (des vraies) et rien d'autre sur ce site, merci...

Je ferme la discussion