Inégalité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Viko
- Membre Relatif
- Messages: 209
- Enregistré le: 18 Juin 2017, 23:51
-
 par Viko » 26 Juil 2017, 19:51
par Viko » 26 Juil 2017, 19:51
Bonjour,
Je cherche à montrer que
 \in \mathbb{R}^{*+}^3)
et
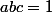
et
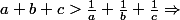
exactement un des réels a, b et c et strictement supérieur à 1
tout sa,
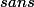
me servir des multiplicateur de Lagrange
j'ai donc penser à utiliser l'identité de Gauss (puisque le but de l'exercice précédent était de la démontrer), l'identité de Gauss est la suivante :
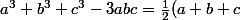((a-b)^2+(b-c)^2+(a-c)^2))
comme ici on a
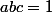
on obtient que :
-6}{(a-b)^2+(b-c)^2+(a-c)^2})
mais je ne sais pas vraiment comment poursuivre....
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
-
Arbre
 par Arbre » 26 Juil 2017, 20:06
par Arbre » 26 Juil 2017, 20:06
Bonjour,
on a :
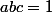
donc
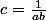
Donc l'inéquation devient :
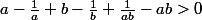
c'est à dire :
(\frac{1}{b}-1)-(a-1)(b-1)>0)
c'est à dire :
(\frac{1}{b}-1)>(a-1)(b-1))
c'est à dire (car on ne peut pas avoir a=1 ou b=1, car sinon on n'aurait pas l'inégalité stricte)
}>\frac{b(b-1)}{1-b})
ssi
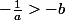
,
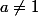
et
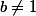
ssi
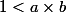
,
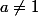
et
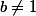
ce sont des équivalences.
Cordialement.
-
Viko
- Membre Relatif
- Messages: 209
- Enregistré le: 18 Juin 2017, 23:51
-
 par Viko » 26 Juil 2017, 20:49
par Viko » 26 Juil 2017, 20:49
j'étais en effet arriver à cette inégalité de mon côté mais je ne vois absolument pas comment la prouver sans utiliser les multiplicateur de Lagrange, une piste peut-être ? (désolé si mes questions peuvent paraitre naïve mais je suis un grand débutant en ce qui concerne ce genre d'inégalité)
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
-
Arbre
 par Arbre » 26 Juil 2017, 21:05
par Arbre » 26 Juil 2017, 21:05
Où vois tu que j'ai utilisé les multiplicateurs de Lagrange ?
Je n'ai fait qu'une factorisation, à aucun moment je n'ai dérivée quoique cela soit, je n'ai pas fait de calcul diff, donc j'ai encore moins utilisé les multiplicateurs de Lagrange.
-
Viko
- Membre Relatif
- Messages: 209
- Enregistré le: 18 Juin 2017, 23:51
-
 par Viko » 26 Juil 2017, 21:20
par Viko » 26 Juil 2017, 21:20
je n'ai pas dit que tu l'avais utiliser ! je te demandais simplement comment prouver que
(\frac{1}{b}-1)>(a-1)(b-1))
sans s'en servir justement, mais ton post éditer réponds à ma question, merci beaucoup j'ai par ailleurs trouvé un moyen détourner pour résoudre ce problème entre temps, il suffit de considérer le polynôme
=(x-a)(x-b)(x-c))
qu'on développe pour obtenir
= x^3-x^2(a+b+c) +x(ab+bc+ac)-abc)
ainsi on a d'une part :
=(1-a)(1-b)(1-c))
et de l'autre
= 1-(a+b+c) +ab+bc+ac-abc)
qui,comme
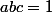
, se simplifie par
=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-a-b-c)
l'inégalité
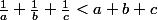
implique évidement que
<0)
on a donc
(1-b)(1-c)<0)
on a alors les trois réels a, b et c supérieur à 1 ou un seul d'entre eux mais l’hypothèse
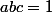
exclue la première possibilité on a donc nécessairement un seul des trois nombres strictement supérieur à 1
encore merci pour ton aide !
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
-
Arbre
 par Arbre » 26 Juil 2017, 21:27
par Arbre » 26 Juil 2017, 21:27
Bizarre. Apprendre à se tromper fait partie des maths.
Au revoir.
-
Viko
- Membre Relatif
- Messages: 209
- Enregistré le: 18 Juin 2017, 23:51
-
 par Viko » 26 Juil 2017, 21:29
par Viko » 26 Juil 2017, 21:29
qu'est-ce qui est bizzare ?
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
-
Arbre
 par Arbre » 26 Juil 2017, 21:34
par Arbre » 26 Juil 2017, 21:34
Je n'ai pas l'impression d'avoir édité quoi que cela soit (dans mon premier message), aprés ton message ton deuxième message.
Deplus on a directement : a+b-a*b-1/a-1/b+1/(a*b)=(1-1/a)*(1-1/b)-(1-a)*(1-b) suffit de développer pour le voir pas besoin de multiplicateur de Lagrange.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités