Espace métrique

[Yasmiiine]

Bonjour,j'arrive pas à démontrer ce théorème,un peu d'aide s'il vous plait?
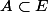
Soit (E,d) un espace métrique,, A ∅
A fermé dans E Pour toute suite convergente (Un) de A vers U dans E ; UA

Alors,pour la première (normalement c'est bon ?) :

A fermé dans E Pour toute suite convergente (Un) de A vers U dans E ; U A

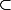
Supposons que A est fermé dans E,Un A et (Un) converge vers U et montrons que U A :
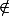
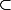
Supposons que U A U C A (complémentaire de A) il existe r > 0 tq : B(U,r) complémentaire de A
D'un autre coté on a (Un) qui converge vers U c'est à dire : il existe n' N , Un B(U,r) , quelque soit n n'
donc : Un complémentaire de A = ∅ ,contradiction donc U A
Est-ce que c'est juste ? y a t-il d'autres méthodes ? Une idée ?

Pour la deuxième :

Pour toute suite convergente (Un) de A vers U dans E ; U A A fermé dans E :

Supposons que U A , UnA et que (Un) converge vers U et montrons que A est fermé dans E c'est à dire on doit montrer qu'il existe U A quelque soit r > 0 : B(U,r) n'est pas inclus dans A

et après je bloque ?? des idées s'il vous plait?

[Arbre]

Bonjour,

Montre que le complémentaire de A est ouvert.

Pourquoi ainsi c'est plus simple, car on définie les fermées à partir de ouverts, donc ce que tu connais vraiment ce sont les ouverts.

Bonne journée.

[Arbre]

Soit x qui n'est pas dans A.
Il faut montrer qu'il existe r>0, tel que B(x,r) est disjoint avec A.
Par l'absurde si cela n'était pas le cas, quelles en seraient les conséquences ?

[Yasmiiine]

Bonjour,

Montre que le complémentaire de A est ouvert.

Pourquoi ainsi c'est plus simple, car on définie les fermées à partir de ouverts, donc ce que tu connais vraiment ce sont les ouverts.

Bonne journée.

C'est ce que j'allais montrer au début mais le complémentaire de A est ouvert cela veut dire que : Quelque soit U Complémentaire de A , il existe r > 0 tq : B(U,r) Complémentaire de A mais on a U A y a une contradiction j'ai pas compris ?!

Soit x qui n'est pas dans A.
il existe r>0, tel que B(x,r) est disjoint avec A.

Pourquoi?

[Arbre]

C'est parce que il faut montrer que le complémentaire de A est un ouvert, et donc pour tout point du complémentaire ou peut trouver une boule ouverte centré en le point qui est tout entière dans le complémentaire.

[Yasmiiine]

Alors :

Supposons que U A , on sait que : A= ,

n'est pas inclus dans A donc il existe U , U A
U Quelque soit r>0 , B(U,r)
Il existe U' A ; d(U;U')< r
et après ? c'est juste au moins ou bien ça mène nul part ? une idée s'il vous plait ?
Merci pour votre aide!

[Arbre]

un conseil pratique :

écrire explicitement ce que l'on veut montrer : ici on dirait que tu veux montrer que l'adhérence de A est A par l'absurde.