Equation trigonometrique : Calcul predictif de cap

[Alvin]

Bonjour à tous !
J'ai quelques soucis à résoudre un problème. Voici l'énoncé :
Soit un navire P0 ayant pour position (x0, y0) dans un repère. Il se déplace à vitesse v0 selon le cap k0.
Soit un navire P1 ayant pour position (x1, y1) dans ce même repère. Il se déplace à une vitesse v1.
Quel cap doit emprunter P1 pour qu'a une certaine date t, P0 et P1 est la meme position ?

( Le cap est donné en radians. La petite différence est que la direction Nord correspond au cap 0, la direction Est au cap PI/2, la direction Sud au cap PI et la direction Ouest au cap 3*PI/2. Ainsi la position (x', y') du navire P0 à date t' est donnée par :
x' = x0 + v0 * t' * sin(k0)
y' = y0 + v0 * t' * cos(k0) )


J'ai différencié 3 cas :
cas où x0 = x1
cas où y0 = y1
cas ou x0 différent de x1 et y0 différent de y1

mais hélas j'arrive à une réponse multiple et je ne parviens à trouver quelle réponse est correcte (il me semble même qu'aucune de mes réponses ne l'est)...

Merci pour votre aide !

PS : si ça peut vous aidez, je peux poster ma résolution (qui malheuresement doit comporter une/des erreurs mais lesquelles... :hum: )

[Quidam]

Bonsoir,
Dans un premier temps, je traiterais ce problème d'un point de vue géométrique pur.

Soit B la position de P0 au départ, A, celle de P1. On connaît le cap K0 de P0, donc on sait qu'il se déplace en ligne droite sur une droite connue.
Soit M le point de rencontre.
Les trajets MA et MB sont proportionnels aux vitesses v1 et v0. Donc on sait que MA/MB = v1/v0.
Or le lieu des points tels que MA/MB soit égal à une constante donnée est le cercle dont un diamètre est défini par les deux points divisant AB selon un rapport égal à cette constante.

Je déterminerais donc la position de ces deux points. Ensuite, l'équation du cercle en question, puis le point de la droite support de la trajectoire de P0 qui coupe le cercle, et qui se trouve dans la direction du cap K0 : il n'y en a qu'un !

Et à la fin, par trigonométrie du triangle, je déterminerai les trois angles du triangle AMB, et enfin le cap, par comparaison avec le cap connu K0 de BM.

Ca a l'air compliqué, mais je ne vois pas d'autre moyen. Ta méthode peut marcher, mais le problème est la détermination de celui des deux points que tu trouveras qui sera le bon ! Avec la méthode ci-dessus, en définissant la droite BM par une équation paramétrique : ( 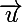définissant le cap K1) et en cherchant les intersections avec le cercle, on trouvera aussi deux solutions, mais on saura distinguer l'intersection passée () de l'intersection avenir().

[Alvin]

Merci beaucoup pour ta réponse !
Hélas, il y a un petit truc que je ne comprend pas... Le passage " dont un diamètre est défini par les 2 points divisant AB selon un rapport à cette constante" reste obscur pour moi...
Merci d'éclairer ma lanterne !

[Alvin]

J'en profite pour poster ma résolution de ce problème qui présente des erreurs... mais lesquelles ? Si quelqu'un parvient à les déceler, merci de m'en faire part !

Enoncé :
Soit un plastron P0 ayant pour position (x0,y0) et se déplaçant à vitesse v0 selon le cap k0.
Soit un plastron P1 ayant pour position (x1,y1) et se déplaçant à vitesse v1.
Quel cap k1 le plastron P1 doit-il emprunter pour qu'à une certaine date t, les plastrons P0 et P1 atteignent la même position M(x,y) ?

Résolution du problème :
[CENTER]x = x0 + v0 * t * sin(k0)
y = y0 + v0 * t * cos(k0)[/CENTER]

A la date t le plastron P1 se trouve à la position :
[CENTER]x = x1 + v1 * t * sin(k1)
y = y1 + v1 * t * cos(k1)[/CENTER]

Les plastrons occupent la même position, on a donc :
[CENTER]x0 + v0 * t * sin(k0) = x1 + v1 * t * sin(k1)
y0 + v0 * t * cos(k0) = y1 + v1 * t * cos(k1)[/CENTER]

Et cela à la même date t, d'où :
[CENTER]t * (v1 * sin(k1) – v0 * sin(k0)) = x0 – x1
t * (v1 * cos(k1) – v0 * cos(k0)) = y0 – y1

t = (x0 – x1) / (v1 * sin(k1) – v0 * sin(k0))
t = (y0 – y1) / (v1 * cos(k1) – v0 * cos(k0))

(x0 – x1) / (v1 * sin(k1) – v0 * sin(k0)) = (y0 – y1) / (v1 * cos(k1) – v0 * cos(k0))[/CENTER]





Cas x0 != x1 et y0 != y1 :

On a ainsi :

[CENTER](x0 – x1) ( v1 * cos(k1) – v0 * cos(k0) ) = (y0 – y1) ( v1 * sin(k1) – v0 * sin(k0) )

cos(k1) – v0/v1 * cos(k0) = (y0 – y1)/(x0 – x1) * ( sin(k1) – v0/v1 * sin(k0) )

cos(k1) – (y0 – y1)/(x0 - x1) * sin(k1) = (v0/v1) * (cos(k0) – (y0 – y1)/(x0 – x1) sin(k0))[/CENTER]

En posant :
[CENTER]a = 1, b = - (yo – y1)/(x0 – x1) et c = (v0/v1) * ( cos(k0) + b * sin(k0)), on obtient :

a * cos(k1) + b * sin(k1) = c[/CENTER]


Résolution de l'équation a * cos(x) + b * sin(x) = c :

Posons tan phi = b / a avec phi appartenant à ]-PI/2 ; PI/2[

On a ainsi :
[CENTER]a * cos(x) + b * sin(x) = a * ( cos(x) + tan phi * sin(x) )
= a * ( cos(x) + sin(;);)phi)/cos(phi););)* sin(x) )
= a / cos(phi) * (cos(x) * cos(phi) + sin(x) * sin(phi))
= a / cos(phi) * cos(x – phi)[/CENTER]

On obtient :
[CENTER]a / cos(phi) * cos(x – phi) = c
cos(x – phi) = c/a * cos(;)phi)[/CENTER]

De la même manière on obtient :
[CENTER]b / cos(phi) * sin(x + phi) = c
sin(x + phi) = c/b * cos(phi);)[/CENTER]


La résolution de ces deux équations

[CENTER]cos(x – phi) = c/a * cos(phi)
sin(x + phi) = c/b * cos(phi);)[/CENTER]

nous permet de lever l'incertitude sur le cap à rallier.

[CENTER] x – phi = { acos( c/a * cos(phi) )
{ - acos( c/a * cos(phi) )

x + phi = { asin( c/b * cos(phi) )
{ PI - ;);)asin( c/b * cos(phi) )



x = { acos( c/a * cos(phi) ) + phi
{ - acos( c/a * cos(phi) ) + phi

x = { asin( c/b * cos(phi) ) - phi
{ PI -;) asin( c/b * cos(phi) ) - phi[/CENTER]

La réponse commune est donc l'unique solution à ce problème.

Cas x0 = x1 :

On a :
[CENTER]t * ( v1 * sin(k1) – v0 * sin(k0) ) = 0[/CENTER]

Or t != 0 d'où
[CENTER]v1 * sin(k1) – v0 * sin(k0) = 0[/CENTER]
Ainsi
[CENTER]sin(k1) = v0/v1 * sin(k0)

k1 = { asin( v0/v1 * sin(k0) )
{ PI - ;);););)asin( v0/v1 * sin(k0) )[/CENTER]

Reste à lever l'incertitude.


Cas y0 = y1 :

On a :
[CENTER]t * ( v1 * cos(k1) – v0 * cos(k0) ) = 0[/CENTER]

Or t != 0 d'où
[CENTER]v1 * cos(k1) – v0 * cos(k0) = 0[/CENTER]
Ainsi
[CENTER]cos(k1) = v0/v1 * cos(k0)

k1 = { acos( v0/v1 * cos(k0) )
{ - ;);)acos( v0/v1 * cos(k0) )[/CENTER]

Reste à lever l'incertitude.




Merci d'avance pour votre aide !

[Quidam]

Merci beaucoup pour ta réponse !
Hélas, il y a un petit truc que je ne comprend pas... Le passage " dont un diamètre est défini par les 2 points divisant AB selon un rapport à cette constante" reste obscur pour moi...
Merci d'éclairer ma lanterne !

Si M appartient à (AB) et que . On dit que M divise AB selon le rapport . Si est différent de 1, il existe deux tels points sur (AB) : l'un est sur le segment AB, l'autre à l'extérieur de AB.

On peut préciser cette notion avec les valeurs algébriques ; pour un et différent de 1, il existe un point sur (AB) à l'extérieur de AB tel que et il existe un point sur (AB) à l'intérieur de AB tel que . On dit que l'ensemble des quatre points forment une division harmonique : mais je pense que ce n'est plus dans les programmes d'avant BAC depuis belle lurette.

On peut aussi utiliser la notion de barycentre. Pour un et différent de 1, il existe un point sur (AB) à l'extérieur de AB tel que et il existe un point sur (AB) à l'intérieur de AB tel que .

Les deux points définis de l'une de ces trois manières sont les mêmes dans les trois cas.

Pour revenir à ton problème, si tu cherches l'ensemble des points du plan tels que , tu n'as qu'à chercher l'unique point I tel que , l'unique point J tel que . Ces deux points I et J appartiennent évidemment à (AB). L'ensemble des points cherchés est le cercle de diamètre IJ !