Inégalités

par **sue** » 23 Oct 2006, 21:21

salut,

je cherche à prouver ces 2 inégalités pour terminer qq exos :

1)

2)

des pistes ?

MERCI

par **drazala** » 23 Oct 2006, 21:56

Pour la première question enlève la valeur absolue pour avoir une double inégalité

.
Ensuite tu sépares les deux inéquations et étudie par exemple :

la tu étudies les variations de la fonction (ici on passe par la dérivée seconde) et le tableau de variations donne le résultat.
Même chose pour l'autre inéquation.

Pour la question 2 pareil tu sépares les deux inéquations et passe tout du même côté, et étudie à nouveau les variations dela fonction correspondante (ici la dérivée première suffit) et le tableau de variations donne le résultat.

Remarque d'ordre général : pour montrer une inégalité entre deux fonctions
f < g, on etudie les varaitions de f-g pour pouvoir avoir le signe.

Drazala

par **sue** » 23 Oct 2006, 22:25

merci drazala ..

mais pour la 1re je crois avoir trouvé une autre méthode :

on a

et

donc

meme chose pour l'inégailté à gauche je crois .

est-ce juste ?

par **Imod** » 23 Oct 2006, 22:34

Je ne suis pas drazala mais je ne trouve rien à redire à ce que tu as fait .

Imod

par **sue** » 23 Oct 2006, 22:45

salut Imod ,

en fait , je crois que c'est pas si évident pour l'autre coté :

et j'ai pas l'habitude de travailler comme m'a montré drazala .

pourriez -vous m'aidez ?

par **rene38** » 23 Oct 2006, 23:04

Bonsoir

sue a écrit:...
est-ce juste ?

Oui mais ça s'obtient sans calcul :
le premier membre est positif (un cosinus est inférieur ou égal à 1) et le second membre est négatif.

par **sue** » 23 Oct 2006, 23:11

oui oui vous avez raison :marteau:
sinon comment ferais-je pour l'autre coté ?

par **sue** » 24 Oct 2006, 19:47

salut,

drazala , pourriez-vous m'expliquer comment démontrer la 1ère inégalité avec ta méthode , j'ai jamais raisonné ainsi :triste:

merci

par **drazala** » 24 Oct 2006, 21:36

Tu poses f(x) = cos(x)-1+

.
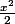
Alors f'(x)=-sin(x)-x et f''(x)=-cos(x)+1
onc f'' est clairement positive (cos(x) entre 1 et -1) donc f' est croissante.
Or f'(0)=0donc f'(x) est positive quand x positive et négative si x négative (fais le tableau de variations de f' en placant f'(0) pour en être convaincue).
Maintenant que tu as le signe de f', fais le tableau de variations de f qui admet du coup un minimum pour x=0.
Donc pour tout x réel f(x) >= f(0) or f(0)=0.
donc pour tout x f(x) >= 0.
Et tu en déduis ton inégalité.

C'est pas l'exemplele plus simple car je suis allé jusqu'à la dérivée seconde.
Pour ta deuxième question même technique mais la dérivée première est suffisante (le signe s'étudie bien)

drazala

par **sue** » 24 Oct 2006, 23:03

salut,
merci bcp je crois que j'ai compris ta méthode :we:
voilà ce que je trouve pour la 2ème : posons

----------
on a

donc

et

, il se voit trés bien mnt que f admet un maximum en

, don c

or

donc :

cqfd .
meme chose pour le membre à gauche .
----------
est-ce bon ?

par **drazala** » 25 Oct 2006, 06:03

parfait :we:

drazala

Inégalités

inégalités

Qui est en ligne