Problème de Limite

[Viko]

Bonjour,

Aujourd'hui au détour d'un exercice j'ai été amené à déterminer la limite en de :
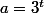
en posant et en utilisant le fait que en : j'ai réussi à déduire que et donc que mais quand il s'agit de trouver une "vrai" démonstration je sèche complétement, quelqu'un aurait-il une idée ?

[pascal16]

Je ne suis pas un spécialiste, mais tu multiplies par 3^(t-1) qui devient très grand quand t devient grand, donc il faut prendre des précautions.

tu peux dire que (x/3^t) tend vers 0 quand t tend vers l'infini
à x fixé, c'est comme une constante (non nulle), c'est t qui est important dans l'écriture
donc sin (x/3^t) = x/3^t + o(1/3^t)
donc 3^(t-1)sin (x/3^t) = x/3+ o(1)
x/3 est une constante, le reste est en o(1), donc négligeable devant la constante

[aviateur]

Bonjour
On ne peut pas dire qu'il faut une vraie démonstration mais plutôt une bonne justification qui utilise
les connaissances de bases: Grosso modo la justification tu l'as donnée mais on détaille un peu pour être convaincu.

D'abord on met x=0 à part. Ensuite la fonction est paire par rapport à la variable x donc on va supposer que x>0.

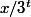
Maintenant on raisonne à x fixé: tend vers 0 et comme en u =0
on a bien

On peut utiliser maintenant les règles "des équivalents" (produits, quotients)



c.q.f.d

[aviateur]

pardon je n'ai pas vu le message de pascal16.

[aviateur]

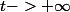
bien entendu dans ma réponse il faut savoir dire que l'équivalent est en quand c'est le cas;

[Viko]

Merci à tout les deux ! je poursuis mon exercice maintenant....