Suite arithmétique

[katrena99]

Enoncé:
Soit la suite (Un) définie sur IN* et telle que : la somme Sn du premier jusqu'au nième terme, Sn= 1/2(3n²+2n)
Question : calculer Un en fonction de n, en déduire que U est une suite arithmétique.

Je peux à la limite prouver que Un est arithmétique:
je calcule Sn avec n=1 ensuite avec n=2 je soustrait U1 de la deuxième somme, enfin je fais la soustrction (U2-U1) j'obtiens une constante ce qui prouve que la suite est arithmétique.

merci de m'aider.

[Quidam]

Je peux à la limite prouver que Un est arithmétique:
je calcule Sn avec n=1 ensuite avec n=2 je soustrait U1 de la deuxième somme, enfin je fais la soustrction (U2-U1) j'obtiens une constante ce qui prouve que la suite est arithmétique.

merci de m'aider.

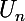
Cela ne suffit pas ! Il va de soi que quelle que soit la suite , la différence ne dépend pas de n ! Par conséquent, la vérification que tu as faite ne sert à rien : elle ne te permet pas de conclure !

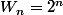
Par exemple, considère la suite . Il est clair que cette suite n'est pas arithmétique : , , ...

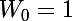
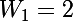
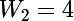
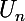
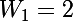
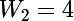
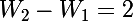
Mais si tu te contentes de faire la même vérification que celle que tu as faite sur et que tu dis : [INDENT]J'ai calculé , j'ai calculé , la différence : c'est une constante, donc la suite est arithmétique[/INDENT] alors tu fais erreur !

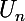
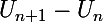
Pour vérifier que ta suite est arithmétique, il faut que tu calcules , puis , que tu calcules la différence et que tu constates que le résultat ne dépend pas de n !

[johnjohnjohn]

Je peux à la limite prouver que Un est arithmétique:
je calcule Sn avec n=1 ensuite avec n=2 je soustrait U1 de la deuxième somme, enfin je fais la soustrction (U2-U1) j'obtiens une constante ce qui prouve que la suite est arithmétique.

merci de m'aider.

Et pour déterminer Un , il faut que tu te souviennes que Sn c'est la somme des n premiers terme de la suite U(n). La réponse est ( presque ) dans la question !

réfléchis dis nous tes conclusions et on te file un autre coup de main si besoin est ...

[katrena99]

je ne sais pas ce qui m'a pris :doh:
regardez plutôt ça :
Sn est la somme de n termes consécutifs,
Un= Sn - S(n-1)
je developpe jusqu'à obtenir Un= (-5/2) + 3n
j'en déduis qu'il s'agit d'une SA car c'est la forme générale d'une SA
correct ?
merci.

[Quidam]

je ne sais pas ce qui m'a pris :doh:
regardez plutôt ça :
Sn est la somme de n termes consécutifs,
Un= Sn - S(n-1)
je developpe jusqu'à obtenir Un= (-5/2) + 3n
j'en déduis qu'il s'agit d'une SA car c'est la forme générale d'une SA
correct ?
merci.

Pas le temps de vérifier !
Mais conclure "il s'agit d'une SA " de "Un= (-5/2) + 3n" est correct !

[johnjohnjohn]

je ne sais pas ce qui m'a pris :doh:
regardez plutôt ça :
Sn est la somme de n termes consécutifs,
Un= Sn - S(n-1)
je developpe jusqu'à obtenir Un= (-5/2) + 3n
j'en déduis qu'il s'agit d'une SA car c'est la forme générale d'une SA
correct ?
merci.

Bahhhh ouééééé lol

pour tout n de N/n>0, Un+1 - Un = 3


Correct

[drazala]

Oui c'est ça à une petite erreur de calcul près la constante est -1/2 d'après mes calculs.
Précise alors le premier terme et la raison.

Un petit truc pour vérifier ton résultat : S1=U1 (somme du premier terme au ... premier terme) donc ta formule pour n=1 doit donner le même résultat entre celle obtenue pour U1 et celle donnée pour S1. Ca ne te garantit pas que c'est juste mais si tes résultats sont différents tu es sûre d'avoir fait une erreur :)

drazala

[katrena99]

j'en déduis qu'il s'agit d'une SA car c'est la forme générale d'une SA

on diraît que je fais expres!
je n'ai qu'à faire U(n+1)-Un ! d'après mes calculs ça donne r=3
PS: comment vous faites ces images contenant les caractères mathématiques et les indices et exposants et ...

[drazala]

Ta première méthode me parait plus adaptée à la question car on te dit : trouver en fonction de n puis en déduire qu'elle est arithmétique...

Pour les images on insère du texte en LATEX traitement de texte mathématiques pour les indices par exemple tu clic sur le bouton TEX et dans la fenêtre qui s'ouvre tu tape u_n et ca te donne

drazala

[katrena99]

Ta première méthode me parait plus adaptée à la question car on te dit : trouver en fonction de n puis en déduire qu'elle est arithmétique...

Pour les images on insère du texte en LATEX traitement de texte mathématiques pour les indices par exemple tu clic sur le bouton TEX et dans la fenêtre qui s'ouvre tu tape u_n et ca te donne

drazala

non non c'est bien ça, j'ai répondu dans l'ordre et c'est ok
et puis merci pour l'info ! ++