Soit A une partie de N, travail sur les ensembles

[ClémentMercier1601]

Bonjour à toutes et tous et merci d'avance à ceux qui prendront le temps de me répondre,
je vous écrit plus bas l'énoncé d'un exercice à propos du quel je joindrai mon travail scanné.
Je pense avoir "saisi l'idée" mais malgré cela je sens un vide dans ma rédaction, je vous prie d'éclairer ma lanterne.

Enoncé:
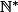
Soit une partie de contenant 1 et telle que :
i) et ii)

a) Montrer que : .
b) Montrer finalement que :

[Viko]

la question a) c'est good je pense, par contre la b je comprends ce que tu as voulu dire mais c'est trés mal dit essaie de revoir cette partie ^^

[zygomatique]

salut

c'est très mal rédigé ... beaucoup de blabla pour rien

soit la propriété

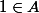
initialisation : et donc P(0) est vraie

hérédité : supposons que P(m) est vraie :

alors d'après i/ donc P(m) => P(m + 1)

conclusion ...


pour tout entier n (non nul) il existe un entier m tel que

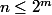
or donc d'après ii/

...

[ClémentMercier1601]

Merci de te réponse !!
Alors en fait j'essayais de dire que comme on montré que 2^m était inclus dans A pour tout m entier naturel.
Donc si m est très très grand ( l'infini) 2^m est toujours dans A et vaut aussi l'infini, or on sait que si un nombre entier appartient à A cela signifie que le nombre qui le précède appartient également à A. Donc si un très très grand nombre appartient à A (l'infini) tout les nombres qui le précédent appartiennent à A, d'où A={1,..,..,..,+inf} = N*
Merci à toi zigomatyque j'ai pas eu l'idée d'une récurrence en fait ^^ je comprends pas du tout ta dernière ligne pour répondre à la question 2

[Viko]

oui c'est ce que je dis l'idée est "bonne" mais c'est trés maladroit... tu as juste à dire que d'aprés ii si un entier est dans A alors tout les entier qui sont inférieur à cette entier sont dans A et comme pour tout m, 2^m est dans A et que pour tout n il existe p tel que n < 2^p on en conclue que tout les entier non nul sont dans A
Enfin comme A est inclus dans N on en conclut que A est bel et bien égale à N*

[zygomatique]

que de fautes de français ...

[Viko]

[ClémentMercier1601]

Effectivement, après relecture je m'auto-pique les yeux... Fin, merci à vous tous de votre aide/vos conseils