soit
Nombres complexes
7 messages
- Page 1 sur 1
nombres complexes
Bonjour, j'aurai besoin de piste pour demarrer cet excercice:
soit = (\cos(\alpha) + z\sin(\alpha))^n - \cos(n\alpha) -i\sin(n\alpha)) . Montrer que
. Montrer que
) est divisible par
est divisible par 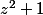 .
.
soit
Re: nombres complexes
Salut,
Calcule P(i) et P(-i), et tu te rendras compte que ce n'est pas vrai.
Cordialement.
Calcule P(i) et P(-i), et tu te rendras compte que ce n'est pas vrai.
Cordialement.
Re: nombres complexes
Alors  = (\cos(\alpha) + i\sin(\alpha))^n -\cos(n\alpha) -i \sin(n\alpha)) , en utilisant la formule de Moivre on aura:
, en utilisant la formule de Moivre on aura:
 = (\cos(n\alpha) + i\sin(n\alpha) -\cos(n\alpha) - i\sin(n\alpha)) ce qui nous donne
ce qui nous donne
 = 0) .
.
pour , le calcul de
, le calcul de ) est un peu bizarre mais par contre voilà ce que j'ai fait:
est un peu bizarre mais par contre voilà ce que j'ai fait:
 = (\cos(\alpha) + z\sin(\alpha)^n -(\cos(\alpha) -i \sin(\alpha))^n)
en utilisant la formule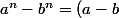(a^{n-1}+...) on aura alors
on aura alors
 = (\cos(\alpha) + z\sin(\alpha) - \cos(\alpha) +i \sin(\alpha))Q(z)) donc
donc
 = (z+i)sin(\alpha)Q(z)) donc P est divisible par
donc P est divisible par 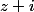 .
.
je peux donc conclure que P est dividible par
pour
en utilisant la formule
je peux donc conclure que P est dividible par
Re: nombres complexes
salut
il y a une faute de signe ...
 = (\cos a + z \sin a)^n - (\cos na + i \sin na) = (\cos a + z \sin a)^n - (\cos a + i \sin a)^n)
il est donc évident que P(i) = 0
il est donc évident que P(-i) <> 0
...
il y a une faute de signe ...
il est donc évident que P(i) = 0
il est donc évident que P(-i) <> 0
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: nombres complexes
vous avez raison, il ya une ereur de signe, donc il ya une ereur dans l'enoncé
Re: nombres complexes
non tu as fait une erreur de signe et l'énoncé est faux ... 
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
