Theoreme de l'hospital exo4
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mahdicanada
- Membre Naturel
- Messages: 32
- Enregistré le: 18 Juin 2017, 21:17
-
 par mahdicanada » 21 Juin 2017, 12:01
par mahdicanada » 21 Juin 2017, 12:01
Bonjour
Je suis en train d'etudier le theoreme de l'hospital et j'ai des exercices à resoudre.
j'ai essayé de faire de mon mieux, je vous donne ma solution ,pouvez vous me corriger
Merci
 image upload
image upload image upload
image upload
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 21 Juin 2017, 14:41
par aymanemaysae » 21 Juin 2017, 14:41
Bonjour ;
Dans le calcul de la dérivée de
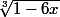
, tu as commis une erreur :
ce n'est pas :
' = ((1-6x)^{-\frac{1}{3}})')
mais
' = ((1-6x)^{\frac{1}{3}})' .)
-
mahdicanada
- Membre Naturel
- Messages: 32
- Enregistré le: 18 Juin 2017, 21:17
-
 par mahdicanada » 21 Juin 2017, 15:09
par mahdicanada » 21 Juin 2017, 15:09
donc la reponse sera comme ca
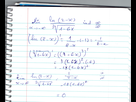
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 21 Juin 2017, 15:46
par aymanemaysae » 21 Juin 2017, 15:46
Bonjour ;
Le résultat est juste .
Une autre méthode :
}{\sqrt[3]{1-6x}} =\dfrac{\ln(2-x)}{\sqrt[3]{-11+6(2-x)}} = \dfrac{\ln(2-x)}{\sqrt[3]{6(2-x)}\sqrt[3]{1-\dfrac{11}{6(2-x)}}} =\dfrac{\ln(2-x)}{\sqrt[3]{6(2-x)}} \dfrac{1}{\sqrt[3]{1-\dfrac{11}{6(2-x)}}}\\\\ \Rightarrow : \lim_{x\rightarrow -\infty} \dfrac{\ln(2-x)}{\sqrt[3]{1-6x}} = \lim_{x\rightarrow -\infty}\dfrac{\ln(2-x)}{\sqrt[3]{6(2-x)}} \dfrac{1}{\sqrt[3]{1-\dfrac{11}{6(2-x)}}} = 0 .)
-
Tiruxa47
- Membre Relatif
- Messages: 343
- Enregistré le: 14 Jan 2017, 16:03
-
 par Tiruxa47 » 22 Juin 2017, 16:51
par Tiruxa47 » 22 Juin 2017, 16:51
Attention à la dérivée du dénominateur, cela donne ceci :
^\frac{1}{3}=\frac{1}{3}\left(1-6x \right)^\frac{-2}{3}(-6)=-2\left(1-6x \right)^\frac{-2}{3}=\frac{-2}{\left(1-6x \right)^\frac{2}{3}}=\frac{-2\left(1-6x \right)^\frac{1}{3}}{1-6x})
-
mahdicanada
- Membre Naturel
- Messages: 32
- Enregistré le: 18 Juin 2017, 21:17
-
 par mahdicanada » 22 Juin 2017, 16:57
par mahdicanada » 22 Juin 2017, 16:57
Tiruxa47 a écrit:Attention à la dérivée du dénominateur, cela donne ceci :
^\frac{1}{3}=\frac{1}{3}\left(1-6x \right)^\frac{-2}{3}(-6)=-2\left(1-6x \right)^\frac{-2}{3}=\frac{-2}{\left(1-6x \right)^\frac{2}{3}}=\frac{-2\left(1-6x \right)^\frac{1}{3}}{1-6x})
effectivement

encore une erreur a cause de travailler tard dans la nuit
Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités



