Pouvez vous me donner une piste pour prouver que:
Intégrale d'une exponentielle
16 messages
- Page 1 sur 1
Re: intégrale d'une exponentielle
Salut !
Avant tout as-tu prouvé que cette intégrale converge ?
Il s'agit d'un calcul classique : pose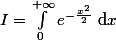 et considère son carré
et considère son carré 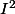 .
.
Tu as alors :
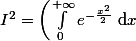^2 <br />= \left( \int_0^{+\infty} e^{- \frac{x^2}{2}}\ {\rm d} x \right) \left( \int_0^{+\infty} e^{- \frac{y^2}{2}}\ {\rm d} y \right))
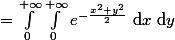
Effectue alors un changement de variables en coordonnées polaires :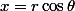 et
et 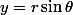 , où
, où  et
et 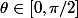 puis utilise la formule de changement de variable (avec la valeur absolue du déterminant de la matrice jacobienne) pour montrer que :
puis utilise la formule de changement de variable (avec la valeur absolue du déterminant de la matrice jacobienne) pour montrer que :
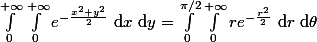) .
.
Tu obtient donc une intégrale que tu sais calculer !
en espérant ne pas avoir fait d'erreurs de calcul, je te laisse poursuivre
Avant tout as-tu prouvé que cette intégrale converge ?
Il s'agit d'un calcul classique : pose
Tu as alors :
Effectue alors un changement de variables en coordonnées polaires :
Tu obtient donc une intégrale que tu sais calculer !
en espérant ne pas avoir fait d'erreurs de calcul, je te laisse poursuivre

- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: intégrale d'une exponentielle
C'est l'intégrale de Gauss ça, c'est super ardu à prouver. Tu as quoi comme outils ?
J'ai cherché un peu à une époque, j'ai laissé tomber.
Ca me donne envie de ré-essayer > http://valentin.vinoles.free.fr/documen ... _gauss.pdf
J'ai cherché un peu à une époque, j'ai laissé tomber.
Ca me donne envie de ré-essayer > http://valentin.vinoles.free.fr/documen ... _gauss.pdf
Modifié en dernier par chombier le 11 Juin 2017, 20:41, modifié 1 fois.
Re: intégrale d'une exponentielle
Merci pour le partage chombier 
D'ailleurs, ton résultat est faux, cette intégrale vaut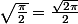

ArtyB a écrit:Bonjour,
Pouvez vous me donner une piste pour prouver que:?
D'ailleurs, ton résultat est faux, cette intégrale vaut
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: intégrale d'une exponentielle
capitaine nuggets a écrit:
Sans oublier que l'interversion est licite par Fubini-Tonelli

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: intégrale d'une exponentielle
Lostounet a écrit:capitaine nuggets a écrit:
Sans oublier que l'interversion est licite par Fubini-Tonelli
Je laisse les détails à notre ami ArtyB mais cela dépend si il a déjà vu ce théorème, ce qui requiert un peu de théorie de la mesure ? Je ne sais pas si on le voit sans théorie de la mesure. Mais bon là on est dans un cadre bien sympathique où les choses "se passent bien".

- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: intégrale d'une exponentielle
capitaine nuggets a écrit:Merci pour le partage chombier
De rien. Je ne suis plus bon à rien, je n'arrive pas à prouver que
je suis trop blasé
Re: intégrale d'une exponentielle
chombier a écrit:capitaine nuggets a écrit:Merci pour le partage chombier
De rien. Je ne suis plus bon à rien, je n'arrive pas à prouver que
je suis trop blasé
x^2 exp(-x^2) tend vers 0 en l'infini donc pour x assez grand, x^2 exp(-x^2) <= 1, c'est-à-dire exp(-x^2)<=x^(-2) pour x assez grand
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: intégrale d'une exponentielle
Pour x assez grand certes, mais là il s'agit de montrer que c'est vrai pour tout x>=1
Re: intégrale d'une exponentielle
chombier a écrit:capitaine nuggets a écrit:Merci pour le partage chombier
De rien. Je ne suis plus bon à rien, je n'arrive pas à prouver que
je suis trop blasé
Pourquoi dis-tu ça, ça fait longtemps que tu n'as plus fait d'intégrales impropres ?
Autre méthode : pour
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: intégrale d'une exponentielle
capitaine nuggets a écrit:chombier a écrit:capitaine nuggets a écrit:Merci pour le partage chombier
De rien. Je ne suis plus bon à rien, je n'arrive pas à prouver que
je suis trop blasé
Pourquoi dis-tu ça, ça fait longtemps que tu n'as plus fait d'intégrales impropres ?
Autre méthode : pour,
donc
.
Mais il ne faut pas comparer
Re: intégrale d'une exponentielle
Bonsoir,
Aussi : pour tout .
.
Donc a fortiori pour tout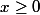 , et pour
, et pour  . Puis on prend les inverses.
. Puis on prend les inverses.
Aussi : pour tout
Donc a fortiori pour tout
Modifié en dernier par Pseuda le 11 Juin 2017, 21:18, modifié 1 fois.
Re: intégrale d'une exponentielle
Avec l'argument que j'ai donné, on a :
 .
.


- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: intégrale d'une exponentielle
chombier a écrit:Pour x assez grand certes, mais là il s'agit de montrer que c'est vrai pour tout x>=1
Ben non, on s'en fout que ce soit pour tout x>= 1 !
Il s'agit d'étudier l'intégrabilité au voisinage de l'infini. Donc une majoration à partir d'un certain rang suffit pour cet exercice!
Et puis en 0 il n'y a aucun problème vu que exp(-x^2/2) est continue en 0.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: intégrale d'une exponentielle
Pseuda a écrit:Bonsoir,
Aussi : pour tout.
Donc a fortiori pour tout, et pour
. Puis on prend les inverses.
Donc,
Merci ! Il me semble pourtant avoir cherché dans cette direction.
Je dois être fatigué !
Re: intégrale d'une exponentielle
Lostounet a écrit:chombier a écrit:Pour x assez grand certes, mais là il s'agit de montrer que c'est vrai pour tout x>=1
Ben non, on s'en fout que ce soit pour tout x>= 1 !
Il s'agit d'étudier l'intégrabilité au voisinage de l'infini. Donc une majoration à partir d'un certain rang suffit pour cet exercice!
Et puis en 0 il n'y a aucun problème vu que exp(-x^2/2) est continue en 0.
Tu as entièrement raison !
Mais j'avais commencé à faire cette fiche : http://valentin.vinoles.free.fr/documen ... _gauss.pdf
J'avais envie de la suivre pas à pas (c'est mon côté borné au voisinage de 0, ça
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
