Algébre linéaire PB

[sammousse]

Bonjour à tous !!

Je suis heureux de faire partie de cette communauté!! car je sens que cette année je vais souvent avoir besoin de vos lumières :we: j'espère bien évidemment pouvoir en apporter (de la lumière)!!!! :id:

Nouvel auditeur au cnam, cela fait plusieurs années que je n'ai pas fais d’algèbre, surtout à ce niveau.....

Ma vie au sein de ce forum commence par une demande d'aide !!

Je n'arrive pas à construire la démarche permettant de répondre à la 1ère question de cet exercice ce qui me bloque grandement.
Pourriez-vous m'aider ?

Voici l'énoncé

Soient les 5 vecteurs de R4 :

V1 = (1, 2,;)2, 1), V2 = (2,;)1, 6,;)13), V3 = (;)1, 2,;)6, 11), V4 = (5, 9,;)8,2), V5 = (1, 4,;)6, 7)

Soit E le sous espace vectoriel engendré par ces 5 vecteurs

1) En combinant linéairement V1 successivement avec V2, V3, V4 puis V5 montrer qu’on obtient un nouveau système de générateurs de E {V1, V 0 2, V 0 3, V 0 4, V 0 5} tel que V 0 2, V 0 3, V 0 4 et V 0 5 aient au moins
une composante nulle de même position ( méthode d’´elimination de Gauss)
.
2) En déduire des relations entre les vecteurs V 0 2, V 0 3, V 0 4 et V 0 5 et donner la dimension de E.

3) Mêmes questions pour le système de 4 vecteurs de R5 :
W1 = (1, 2,;)1, 5, 1), W2 = (2,;)1, 2, 9, 4), W3 = (;)2, 6,;)6,;)8,;)6), W4 = (1,;)13, 11, 2, 7)
4) déduire des calculs du 3) la résolution de l’´equation vectorielle.
1V1 + 2V2 + 3V3 + 4V4 + 5V5 = 0

toutes bribes d'informations m'intéressent !! :we:

Merci !!

[drazala]

Au vu de la question tu dois utiliser le même principe que le pivot de Gauss,c'est à dire utiliser V1 pour annuler une coordonnée le plus simple est d'annuler la première.
On te dit par combinaison linéaire ce qui signifie que tu dois faire un calcul du genre V2- V1 de manière à annuler la première coordonnée de V2 pour obtenir V0 2. de même pour les autres vecteurs. (indic pour V2 ).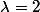
Ensuite un théorème du cours te garantis que le système obtenu est toujours générateur.

drazala

[sammousse]

Histoire de cibler un peu oû je bloque voici mon raisonnement (qui ne va pas trés loin):

Il faut donc que je combine lineairement le vecteur V1 avec V2 V3 V4 V5
Donc
V2'=x1V1+x2V2
V3'=x1V1+x3V3
V4'=x1V1+x4V4
V5'=x1V1+x5V5

Bon la j'applique le cour, mais je ne voix pas ou cela va me mener..... :cry:
HELP

[yos]

1) Tu peux remplacer (V1,...,V5) par (V1, V2-2V1, V3+V1, V4-5V1, V5-V1) histoire de faire sauter la première coordonnée des quatre derniers vecteurs. Il est clair (?) que le second système engendre aussi E.
Si tu fais déjà ces calculs, peut-être verras-tu plus clair pour la suite de l'exercice.

[sammousse]

:we: merci beaucoup je vais voir ca !!!! :we: