Topologie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 07 Juin 2017, 20:08
par kurenay » 07 Juin 2017, 20:08
Bonsoir,
Soit
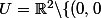\})
. Montrer que U est un ouvert de
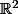
.
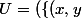\in \R^2 , x>0 \} \cup \{(x,y)\in \R^2 , x<0 \}) \cap (\{(x,y)\in \R^2 , y>0 \} \cup \{(x,y)\in \R^2 , y<0 \}))
.
Est-ce que mon U est juste ? Et pourquoi

Pour montrer ouvert: image réciproque d'ouvert par application continue . Puis union et intersection d'ouvert donc ouvert.
Merci

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 08 Juin 2017, 00:18
par capitaine nuggets » 08 Juin 2017, 00:18
Quel est le complémentaire de

dans

? Est-il fermé ? Qu'en déduis-tu pour

?
\} \ne \mathbb{R}^*\times \mathbb{R}^*)
car
\})
est égal à

privé du point
)
alors que
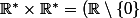 \times (\mathbb{R}\setminus \{0\}))
est égal à

privé des droites
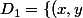\in \mathbb{R}^2\ ;\ x=0 \})
et
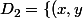\in \mathbb{R}^2\ ;\ y=0 \})
. En fait, puisque
 \in D_1 \cup D_2)
, on a seulement
\} \supsetneq \mathbb{R}^*\times \mathbb{R}^*)
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 08 Juin 2017, 00:26
par kurenay » 08 Juin 2017, 00:26
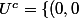\})
fermé car singleton donc U ouvert
Je n'arrivais pas à faire la différence entre ces 2 ensembles mais je comprends mieux maintenant, merci

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
