Différence fonction suite
19 messages
- Page 1 sur 1
Différence fonction suite
Bonjour,
Je souhaite comprendre la réelle différence (ou les) entre fonction et suite (parce que pour moi ce sont des fonctions mais je pense que si elles sont tant "isolées" ce n'est pas pour rien, il y a sûrement quelque chose que je ne perçois pas).
Merci.
Je souhaite comprendre la réelle différence (ou les) entre fonction et suite (parce que pour moi ce sont des fonctions mais je pense que si elles sont tant "isolées" ce n'est pas pour rien, il y a sûrement quelque chose que je ne perçois pas).
Merci.
Sapere Aude
Re: Différence fonction suite
Ah c'est ça la seul différence alors. Je pensais qu'il y avait autre chose que je ne voyais pas.
que n soit dans les Naturels (alors que x dans les R). Ah ok. Juste une fonction particulière.
Merci beaucoup et bon dimanche.
que n soit dans les Naturels (alors que x dans les R). Ah ok. Juste une fonction particulière.
Merci beaucoup et bon dimanche.
Sapere Aude
Re: Différence fonction suite
La différence est qu'une suite a pour domaine de définition les entiers naturels alors qu'une fonction peut-être définie sur un intervalle de R par exemple.
Donc on ne risque pas de 'dériver' une suite.
Donc on ne risque pas de 'dériver' une suite.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Différence fonction suite
Lostounet a écrit:La différence est qu'une suite a pour domaine de définition les entiers naturels alors qu'une fonction peut-être définie sur un intervalle de R par exemple.
Donc on ne risque pas de 'dériver' une suite.
Ah...
Ça m'intéresse.
Je pensais que dérivée (coef directeur de la tangente) c'était fait parce qu'il trop complexe de calculer la tangente de tous les points et en faisant la dérivée on pouvait trouver le signe plus simplement.
Du coup, pourquoi on ne risque pas de dériver une suite (ça sonne comme un interdit ou une impossibilité... et ça m'interroge.)
Pourquoi, même dans les naturels (entiers positifs je crois), on ne pourrait pas avoir de dérivée puisque ce n'est que le coef d'une tangente pour étude de signe ? Je ne comprends pas.
Et au passage si vous êtes ok (je pense que vous avez beaucoup de message ces temps-ci) pourquoi la primitive (aire sous la courbe) est l'inverse (rapport avec x ou : me semble) de la dérivée.
Je ne parviens pas à faire la rapprochement entre la tangente et toute l'aire sous la courbe entre 2 abscisses.
Vaguement je dirais que les tangentes sont sur les points de la courbe mais... ça tilt pas le rapport direct.
Merci
Sapere Aude
Re: Différence fonction suite
Salut !
Géographiquement :
La courbe représentative d'une fonction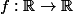 est définie comme étant l'ensemble des points
est définie comme étant l'ensemble des points )) , lorsque
, lorsque  décrit le domaine de
décrit le domaine de 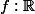 ici. C'est donc quelque chose de "continue".
ici. C'est donc quelque chose de "continue".
Si on devais faire pareil pour une suite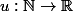 (où on note
(où on note =u_n) ), sa courbe représentative est l'ensemble des points
), sa courbe représentative est l'ensemble des points ) , lorsque
, lorsque  décrit
décrit  . C'est donc une réunion infinie de points, donc pas vraiment "continue" comme le cas précédent.
. C'est donc une réunion infinie de points, donc pas vraiment "continue" comme le cas précédent.
Calculer la dérivée d'une fonction c'est exprimer le coefficient directeur de la tangente en un point quelconque de la courbe représentative. Or comment définir la tangente en un point isolé des autres ?
Algébriquement,
Pour qu'une fonction soit dérivable en un point, il faut que ce point appartiennent à un intervalle ouvert non vide du domaine de définition et que le nombre dérivé de cette fonction en ce point soit fini.
Sachant que ne contient aucun intervalle ouvert, on ne peut pas calculer le nombre dérivé en un point.
ne contient aucun intervalle ouvert, on ne peut pas calculer le nombre dérivé en un point.

Géographiquement :
La courbe représentative d'une fonction
Si on devais faire pareil pour une suite
Calculer la dérivée d'une fonction c'est exprimer le coefficient directeur de la tangente en un point quelconque de la courbe représentative. Or comment définir la tangente en un point isolé des autres ?
Algébriquement,
Pour qu'une fonction soit dérivable en un point, il faut que ce point appartiennent à un intervalle ouvert non vide du domaine de définition et que le nombre dérivé de cette fonction en ce point soit fini.
Sachant que
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Différence fonction suite
la réalité est un peu différente
si on peut exprimer Un=f(n), on peut étudier dans R la fonction f(x), les résultats valables dans R (limite, variations obtenue par dérivée si on veut) le sont dans N par restriction à N de 'ensemble de définition de f.
Dans la vie courante, beaucoup de problèmes sont posés sou forme de suite car les données sont discrètes (intérêts, récolte annuels, population...) D'où l'utilité des suites.
Tu feras sans doute des modèles mathématiques continus pour en étudier les évolutions plus tard.
si on peut exprimer Un=f(n), on peut étudier dans R la fonction f(x), les résultats valables dans R (limite, variations obtenue par dérivée si on veut) le sont dans N par restriction à N de 'ensemble de définition de f.
Dans la vie courante, beaucoup de problèmes sont posés sou forme de suite car les données sont discrètes (intérêts, récolte annuels, population...) D'où l'utilité des suites.
Tu feras sans doute des modèles mathématiques continus pour en étudier les évolutions plus tard.
Re: Différence fonction suite
capitaine nuggets a écrit:Salut !
Géographiquement :
La courbe représentative d'une fonctionest définie comme étant l'ensemble des points
, lorsque
décrit le domaine de
ici. C'est donc quelque chose de "continue".
Si on devais faire pareil pour une suite(où on note
), sa courbe représentative est l'ensemble des points
, lorsque
décrit
. C'est donc une réunion infinie de points, donc pas vraiment "continue" comme le cas précédent.
Calculer la dérivée d'une fonction c'est exprimer le coefficient directeur de la tangente en un point quelconque de la courbe représentative. Or comment définir la tangente en un point isolé des autres ?
Algébriquement,
Pour qu'une fonction soit dérivable en un point, il faut que ce point appartiennent à un intervalle ouvert non vide du domaine de définition et que le nombre dérivé de cette fonction en ce point soit fini.
Sachant quene contient aucun intervalle ouvert, on ne peut pas calculer le nombre dérivé en un point.
Ah ! Je crois que ça vient de comprendre (si c'est ça j'ai presque honte d'avoir demandée lol mais j'ai bien fait, sinon j'aurais pas tilté
En gros, je voyais tous les positifs au lieu de ne voir QUE les entiers (positifs) parce qu'en reliant les points et en ne regardant que les tracés, je voyais quelque chose de continu, une courbe.
Sauf que non, parce qu'il n'y a "rien" (pardon pour l'expression, je veux m'assurer que c'est bien ça) entre les n 2 et 3 par exemple
(contrairement aux fonctions donc où il y a toute l'infinité de décimaux entre les 2.)
Honnêtement, appliquer les formules maintenant dans les exos ça va, mais comprendre pourquoi on le fait de façon bien plus précise, c'est quand même le but !!! (et génial)
Merci pour tout.

Sapere Aude
Re: Différence fonction suite
pascal16 a écrit:Dans la vie courante, beaucoup de problèmes sont posés sou forme de suite car les données sont discrètes (intérêts, récolte annuels, population...) D'où l'utilité des suites.
Merci beaucoup.
Sapere Aude
Re: Différence fonction suite
Bonjour Even33,
Afin de pouvoir répondre à cette question, il faut qu'on revienne à la définition de ce qu'est le nombre dérivé. Ce n'est pas une construction abstraite, bien au contraire !
On part d'une fonction f quelconque (on va supposer pour le moment qu'elle est définie sur tout les réels, c'est-à-dire que f(x) existe pour tout x et on va d'abord supposer en plus que f est une fonction continue: cela signifie que la courbe de f peut être tracée en un seul trait de ton stylo, sans lever ta main).
On se souvient d'abord que si on a deux points dans un repère, disons A(x;y) et B(u;v), (u différent de x) alors la pente de la droite (AB) est le nombre (v-y)/(u - x): on en aura besoin plus tard. Tu es bien d'accord que si une droite a une pente positive, c'est qu'elle est "vers le haut" et que si sa pente est négative, vers le bas?
Donc maintenant je te propose de placer deux points A et B sur la courbe de f comme tu veux et de tracer la droite (AB). Cette droite (AB) peut couper la courbe de f en d'autres points, mais on s'en fiche. Je note a l'abscisse de A et comme A est sur la courbe, son ordonnée est f(a) par définition. Maintenant je vais prendre B "à droite de A", ie je vais prendre son abscisse "a+quelquechose". Ce quelque chose on peut le noter par exemple h, l'abscisse de B devient donc (a + h).
Comme B est sur la courbe aussi, son ordonnée est f(a+h). Si je calcule maintenant la pente de la droite (AB) (avec la formule du dessus) je trouve:
 - f(a)}{(a + h) - (a)})
Maintenant je vais te poser la question suivante, en regardant la courbe de f aux alentours du point A, je veux que tu me dises si f augmente ou diminue.
Premier cas de figure:

(Je regarde ici bien entendu le point a = 6)
Tu constates que B est un peu trop loin et que la droite (AB) est un peu inutile pour répondre à la question ... Donc ce que je vais faire, c'est rapprocher le point B un peu plus. Et si tu te souviens, l'abscisse de B est a+h, je vais donc prendre un h plus petit...
Cela donnera ça:

Et plus j'approche B du point A, plus la droite (AB) me permet de bien "toucher" la courbe de f aux alentours du point A.
Cette action de "rapprocher B" revient à prendre "h" de plus en plus petit, de plus en plus proche de 0 pour avoir B d'abscisse a + h aussi proche de a que possible. On dit qu'on fait tendre h vers 0. On dit aussi "prendre la limite lorsque h s'approche de 0"
Lorsqu'on fait tendre h vers 0, on regarde la pente de la droite (AB) que l'on a calculé plus tard et dans cette formule, on fait tendre h vers 0 pour regarder la pente de (AB) obtenue.
 - f(a)}{(a + h) - (a)})_{h \rightarrow 0})
Si cette pente obtenue une fois h est très petit, est positive, c'est que la droite (AB) a une pente positive et que donc la fonction f est croissante près de A. Si la pente, une fois h rendu petit, est négative, c'est que f décroit.
(AB) est tangente à la courbe car A et B s'approchent jusqu'à presque "se confondre" (donc (AB) ne touchera la courbe qu'en un seul point, à la limite (c'est pas formel ce que je dis mais c'est pour te donner les idées)).
Le (a + h) - a au dénominateur peut être simplifié en "h" tout simplement (pour voir la formule que tu vois dans les livres). Cette quantité est appelée nombre dérivé au point a et qui correspond à ton intuition: celle d'essayer, à l’œil nu, de placer une règle au point A qui touche la courbe et de voir.
Maintenant pour revenir à ta question, pourquoi on ne peut pas dériver une suite? Si on prend la suite:
 = n^2) voici son graphique pour quelques valeurs de n:
voici son graphique pour quelques valeurs de n:

Tu constates que si je veux faire le même travail que plus haut, placer A et B puis rapprocher B je suis bloqué d'office ! Si je mets A d'abscisse 1 (d'ordonnée 1), et que je place B quelque part en (1+ h) sur la "courbe de U(n)" ben je ne peux pas me rapprocher de A en restant sur la courbe de U(n) vu que 1,00001 par exemple n'est pas un entier et qu'on peut pas parler de U(1.00001)... vu qu'une suite n'est définie que pour des entiers naturels.
C'est pour cela que la fonction f de départ est prise au moins continue sur R, pour qu'on puisse bouger B de la manière qu'on veut.
Dans la pratique comme le souligne Pascal, on peut par exemple étudier la fonction f(x) = x^2 puis en déduire des informations sur la suite ( = n^2) ) pour voir si par exemple cette suite est croissante, ou autre. Mais parler de la dérivée de (U(n)) ou écrire U(n) ' est un abus qu'il faut éviter !
) pour voir si par exemple cette suite est croissante, ou autre. Mais parler de la dérivée de (U(n)) ou écrire U(n) ' est un abus qu'il faut éviter !
Attention: le fait que la fonction f soit continue n'assure pas qu'elle possède une dérivée (ie que le nombre dérivé existe en tout point et qu'il soit un nombre fini )! Mais ceci est une autre paire de manches: au lycée, cela arrive rarement.. (sauf pour la fonction racine carrée ou la fonction valeur absolue ) !
) ! 
Concernant ta 2e question, je pense qu'elle mériterait une seconde discussion C'est une bonne question, car le lien n'est pas si "immédiat" ! De grands mathématiciens se sont penchés sur la question;
C'est une bonne question, car le lien n'est pas si "immédiat" ! De grands mathématiciens se sont penchés sur la question;
D'ailleurs, pour comprendre un peu il faut commencer par aborder la notion d'intégrale ! La construction de l'intégrale au lycée est celle qu'a fait le mathématicien Riemann. Il existe aussi un grand théorème que tous les mathématiciens aiment: le théorème fondamental de l'analyse qui fait le lien entre la dérivation et "faire l'inverse", la primitivation. Donc mon conseil: il faut bien saisir les dérivées, puis les primitives puis le calcul d'aires pour comprendre ce lien !
Afin de pouvoir répondre à cette question, il faut qu'on revienne à la définition de ce qu'est le nombre dérivé. Ce n'est pas une construction abstraite, bien au contraire !
On part d'une fonction f quelconque (on va supposer pour le moment qu'elle est définie sur tout les réels, c'est-à-dire que f(x) existe pour tout x et on va d'abord supposer en plus que f est une fonction continue: cela signifie que la courbe de f peut être tracée en un seul trait de ton stylo, sans lever ta main).
On se souvient d'abord que si on a deux points dans un repère, disons A(x;y) et B(u;v), (u différent de x) alors la pente de la droite (AB) est le nombre (v-y)/(u - x): on en aura besoin plus tard. Tu es bien d'accord que si une droite a une pente positive, c'est qu'elle est "vers le haut" et que si sa pente est négative, vers le bas?
Donc maintenant je te propose de placer deux points A et B sur la courbe de f comme tu veux et de tracer la droite (AB). Cette droite (AB) peut couper la courbe de f en d'autres points, mais on s'en fiche. Je note a l'abscisse de A et comme A est sur la courbe, son ordonnée est f(a) par définition. Maintenant je vais prendre B "à droite de A", ie je vais prendre son abscisse "a+quelquechose". Ce quelque chose on peut le noter par exemple h, l'abscisse de B devient donc (a + h).
Comme B est sur la courbe aussi, son ordonnée est f(a+h). Si je calcule maintenant la pente de la droite (AB) (avec la formule du dessus) je trouve:
Maintenant je vais te poser la question suivante, en regardant la courbe de f aux alentours du point A, je veux que tu me dises si f augmente ou diminue.
Premier cas de figure:

(Je regarde ici bien entendu le point a = 6)
Tu constates que B est un peu trop loin et que la droite (AB) est un peu inutile pour répondre à la question ... Donc ce que je vais faire, c'est rapprocher le point B un peu plus. Et si tu te souviens, l'abscisse de B est a+h, je vais donc prendre un h plus petit...
Cela donnera ça:

Et plus j'approche B du point A, plus la droite (AB) me permet de bien "toucher" la courbe de f aux alentours du point A.
Cette action de "rapprocher B" revient à prendre "h" de plus en plus petit, de plus en plus proche de 0 pour avoir B d'abscisse a + h aussi proche de a que possible. On dit qu'on fait tendre h vers 0. On dit aussi "prendre la limite lorsque h s'approche de 0"
Lorsqu'on fait tendre h vers 0, on regarde la pente de la droite (AB) que l'on a calculé plus tard et dans cette formule, on fait tendre h vers 0 pour regarder la pente de (AB) obtenue.
Si cette pente obtenue une fois h est très petit, est positive, c'est que la droite (AB) a une pente positive et que donc la fonction f est croissante près de A. Si la pente, une fois h rendu petit, est négative, c'est que f décroit.
(AB) est tangente à la courbe car A et B s'approchent jusqu'à presque "se confondre" (donc (AB) ne touchera la courbe qu'en un seul point, à la limite (c'est pas formel ce que je dis mais c'est pour te donner les idées)).
Le (a + h) - a au dénominateur peut être simplifié en "h" tout simplement (pour voir la formule que tu vois dans les livres). Cette quantité est appelée nombre dérivé au point a et qui correspond à ton intuition: celle d'essayer, à l’œil nu, de placer une règle au point A qui touche la courbe et de voir.
Maintenant pour revenir à ta question, pourquoi on ne peut pas dériver une suite? Si on prend la suite:

Tu constates que si je veux faire le même travail que plus haut, placer A et B puis rapprocher B je suis bloqué d'office ! Si je mets A d'abscisse 1 (d'ordonnée 1), et que je place B quelque part en (1+ h) sur la "courbe de U(n)" ben je ne peux pas me rapprocher de A en restant sur la courbe de U(n) vu que 1,00001 par exemple n'est pas un entier et qu'on peut pas parler de U(1.00001)... vu qu'une suite n'est définie que pour des entiers naturels.
C'est pour cela que la fonction f de départ est prise au moins continue sur R, pour qu'on puisse bouger B de la manière qu'on veut.
Dans la pratique comme le souligne Pascal, on peut par exemple étudier la fonction f(x) = x^2 puis en déduire des informations sur la suite (
Attention: le fait que la fonction f soit continue n'assure pas qu'elle possède une dérivée (ie que le nombre dérivé existe en tout point et qu'il soit un nombre fini )! Mais ceci est une autre paire de manches: au lycée, cela arrive rarement.. (sauf pour la fonction racine carrée ou la fonction valeur absolue
 ) !
) ! 
Concernant ta 2e question, je pense qu'elle mériterait une seconde discussion
D'ailleurs, pour comprendre un peu il faut commencer par aborder la notion d'intégrale ! La construction de l'intégrale au lycée est celle qu'a fait le mathématicien Riemann. Il existe aussi un grand théorème que tous les mathématiciens aiment: le théorème fondamental de l'analyse qui fait le lien entre la dérivation et "faire l'inverse", la primitivation. Donc mon conseil: il faut bien saisir les dérivées, puis les primitives puis le calcul d'aires pour comprendre ce lien !
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Différence fonction suite
Très très intéressants échanges !! moi aussi Even j'avais tiqué sur le "dérivé" pour une fonction et non pour une suite, maintenant c'est extrêmement clair !! Superbe !! M E R C I !!!!!!!!!!!!!!!!!!!!
Une autre chose me fait réagir : le fait qu'une fonction soit continue n'implique pas qu'elle soit dérivable . . .
j'imagine le cas d'une asymptote verticale et donc les tangentes dans la partie de la courbe partant vers l' se rapprocheraient d'une droite verticale, de pente tendant vers l'
se rapprocheraient d'une droite verticale, de pente tendant vers l'  , c'est ça ? . . .
, c'est ça ? . . .
Je ne visualise pas d'autres cas . . . sinon si la courbe est discontinue, bien sûr en ces endroits il n'y a de tangente donc pas dérivable . . .
Peut-on écrire cela ? :

Une autre chose me fait réagir : le fait qu'une fonction soit continue n'implique pas qu'elle soit dérivable . . .
j'imagine le cas d'une asymptote verticale et donc les tangentes dans la partie de la courbe partant vers l'
Je ne visualise pas d'autres cas . . . sinon si la courbe est discontinue, bien sûr en ces endroits il n'y a de tangente donc pas dérivable . . .
Peut-on écrire cela ? :

Re: Différence fonction suite
@Laetidom
Le défaut de dérivabilité peut venir de "deux" raisons (si on peut dire):
a) Le nombre dérivé tend vers l'infini au point
Considère l'exemple = \sqrt{x}) qui est continue en 0 dont le nombre dérivé en 0 donne:
qui est continue en 0 dont le nombre dérivé en 0 donne:
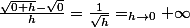
Je ne sais pas si on peut parler ici d'asymptote verticale: la fonction est bien continue en 0 et elle a pas d'asymptote. Toutefois tu peux parler de tangente "verticale"..à voir.
b) Le nombre dérivé n'existe pas
Considère = |x|) qui est continue sur R. Selon comment tu t'approches du point x = 0 (h tend vers 0+ ou 0-), tu auras une limite différente:
qui est continue sur R. Selon comment tu t'approches du point x = 0 (h tend vers 0+ ou 0-), tu auras une limite différente:

Tandis que: Au point 0 on parle de deux demi-tangentes, ou de dérivabilité à droite (resp. gauche).
Au point 0 on parle de deux demi-tangentes, ou de dérivabilité à droite (resp. gauche).
Bien entendu ailleurs qu'en 0, les fonctions ci-dessus sont très dérivables !
Pour les fonctions usuelles, on aura du mal à trouver plus de défauts qu'en quelques points bien choisis: la plupart des fonctions usuelles (polynome, cosinus, sinus, exponentielle) sont dérivables partout sur leurs domaines de définition. Il existe toutefois (c'est ce que tu cherches?) des fonctions continues en tout point mais dérivables en aucun point. Comme pour la fonction pathologique de Weierstrass: https://fr.wikipedia.org/wiki/Fonction_de_Weierstrass
Mais on voit bien qu'elle n'est pas vraiment "usuelle": elle est définie par une série trigonométrique (à chaque x on associe en quelque sorte la valeur d'une somme infinie)
Un autre exemple: la fonction de Thomae. https://fr.wikipedia.org/wiki/Fonction_de_Thomae
Celle-ci peut être rendue dérivable en tout point x irrationnel , mais elle est discontinue sur Q (l'ensemble des rationnels) !
Le défaut de dérivabilité peut venir de "deux" raisons (si on peut dire):
a) Le nombre dérivé tend vers l'infini au point
Considère l'exemple
Je ne sais pas si on peut parler ici d'asymptote verticale: la fonction est bien continue en 0 et elle a pas d'asymptote. Toutefois tu peux parler de tangente "verticale"..à voir.
b) Le nombre dérivé n'existe pas
Considère
Tandis que:
Bien entendu ailleurs qu'en 0, les fonctions ci-dessus sont très dérivables !
Pour les fonctions usuelles, on aura du mal à trouver plus de défauts qu'en quelques points bien choisis: la plupart des fonctions usuelles (polynome, cosinus, sinus, exponentielle) sont dérivables partout sur leurs domaines de définition. Il existe toutefois (c'est ce que tu cherches?) des fonctions continues en tout point mais dérivables en aucun point. Comme pour la fonction pathologique de Weierstrass: https://fr.wikipedia.org/wiki/Fonction_de_Weierstrass
Mais on voit bien qu'elle n'est pas vraiment "usuelle": elle est définie par une série trigonométrique (à chaque x on associe en quelque sorte la valeur d'une somme infinie)
Un autre exemple: la fonction de Thomae. https://fr.wikipedia.org/wiki/Fonction_de_Thomae
Celle-ci peut être rendue dérivable en tout point x irrationnel , mais elle est discontinue sur Q (l'ensemble des rationnels) !
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Différence fonction suite
Bonsoir,
Les fonctions du style f(x)=x sin(1/x) pour x 0 et f(0)=0, sont d'autres cas pathologiques de fonctions continues non dérivables (en 0). Le taux d'accroissement oscille constamment à l'approche de 0.
0 et f(0)=0, sont d'autres cas pathologiques de fonctions continues non dérivables (en 0). Le taux d'accroissement oscille constamment à l'approche de 0.
Sinon, pour en revenir à la question initiale, une autre différence essentielle entre les suites et les fonctions, c'est que les suites peuvent être définies par une relation de récurrence, ce qui est impossible pour les fonctions. Par exemple, la suite définie par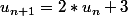 . Cela donne lieu à plein de beaux problèmes où on va chercher à définir le terme général de la suite en fonction de n.
. Cela donne lieu à plein de beaux problèmes où on va chercher à définir le terme général de la suite en fonction de n.
Les fonctions du style f(x)=x sin(1/x) pour x
Sinon, pour en revenir à la question initiale, une autre différence essentielle entre les suites et les fonctions, c'est que les suites peuvent être définies par une relation de récurrence, ce qui est impossible pour les fonctions. Par exemple, la suite définie par
Re: Différence fonction suite
Merci à vous pour ces belles explications complémentaires, riches d'enseignement !!
Bonne journée @ tous !!
Bonne journée @ tous !!
Re: Différence fonction suite
Lostounet a écrit:Bonjour Even33,
Maintenant pour revenir à ta question, pourquoi on ne peut pas dériver une suite? Si on prend la suite:voici son graphique pour quelques valeurs de n:
Tu constates que si je veux faire le même travail que plus haut, placer A et B puis rapprocher B je suis bloqué d'office ! Si je mets A d'abscisse 1 (d'ordonnée 1), et que je place B quelque part en (1+ h) sur la "courbe de U(n)" ben je ne peux pas me rapprocher de A en restant sur la courbe de U(n) vu que 1,00001 par exemple n'est pas un entier et qu'on peut pas parler de U(1.00001)... vu qu'une suite n'est définie que pour des entiers naturels.
C'est pour cela que la fonction f de départ est prise au moins continue sur R, pour qu'on puisse bouger B de la manière qu'on veut.
Dans la pratique comme le souligne Pascal, on peut par exemple étudier la fonction f(x) = x^2 puis en déduire des informations sur la suite () pour voir si par exemple cette suite est croissante, ou autre. Mais parler de la dérivée de (U(n)) ou écrire U(n) ' est un abus qu'il faut éviter !
Attention: le fait que la fonction f soit continue n'assure pas qu'elle possède une dérivée (ie que le nombre dérivé existe en tout point et qu'il soit un nombre fini )! Mais ceci est une autre paire de manches: au lycée, cela arrive rarement.. (sauf pour la fonction racine carrée ou la fonction valeur absolue) !

Concernant ta 2e question, je pense qu'elle mériterait une seconde discussionC'est une bonne question, car le lien n'est pas si "immédiat" ! De grands mathématiciens se sont penchés sur la question;
D'ailleurs, pour comprendre un peu il faut commencer par aborder la notion d'intégrale ! La construction de l'intégrale au lycée est celle qu'a fait le mathématicien Riemann. Il existe aussi un grand théorème que tous les mathématiciens aiment: le théorème fondamental de l'analyse qui fait le lien entre la dérivation et "faire l'inverse", la primitivation. Donc mon conseil: il faut bien saisir les dérivées, puis les primitives puis le calcul d'aires pour comprendre ce lien !
Wahoou !!! Superbe, c'est très très très clair (j'ai pris le temps de bien lire et comprendre, je suis partie hier).
Merci pour tout ces schémas et explications. Limpide, ça permet de bien visualiser.

Sapere Aude
Re: Différence fonction suite
laetidom a écrit:Très très intéressants échanges !! moi aussi Even j'avais tiqué sur le "dérivé" pour une fonction et non pour une suite, maintenant c'est extrêmement clair !! Superbe !! M E R C I !!!!!!!!!!!!!!!!!!!!
Ah ben super ! Si ça peut aider d'autres personnes, j'en suis ravie.
Sapere Aude
Re: Différence fonction suite
Merci Laetidom, la question de la dérivabilité m'est venue en lisant l'explication.
Du coup, merci bcp Lostounet et Pseuda. (même si je ne pense pas pouvoir appliquer là de suite, je comprends au moins pourquoi pourquoi on dit que continue n'est pas = à dérivable obligatoirement.
Merci encore du temps que vous avez pris et bonne journée.
Du coup, merci bcp Lostounet et Pseuda. (même si je ne pense pas pouvoir appliquer là de suite, je comprends au moins pourquoi pourquoi on dit que continue n'est pas = à dérivable obligatoirement.
Merci encore du temps que vous avez pris et bonne journée.
Sapere Aude
Re: Différence fonction suite
Bonjour,
Ce qui différencie fondamentalement les suites des fonctions, c'est la relation de récurrence qu'il y a sur les suites (u(n+1) en fonction de u(n), ...) qu'il n'y a pas sur les fonctions. On peut toujours définir des fonctions en des points isolés de R non régulièrement espacés, cela va faire une fonction discontinue en tout point, nulle part dérivable (car pour être dérivable, une fonction doit être définie sur un intervalle d'intérieur non vide).
Ce qui différencie fondamentalement les suites des fonctions, c'est la relation de récurrence qu'il y a sur les suites (u(n+1) en fonction de u(n), ...) qu'il n'y a pas sur les fonctions. On peut toujours définir des fonctions en des points isolés de R non régulièrement espacés, cela va faire une fonction discontinue en tout point, nulle part dérivable (car pour être dérivable, une fonction doit être définie sur un intervalle d'intérieur non vide).
Re: Différence fonction suite
Salut,
Perso, j'aurais principalement répondu un truc qui va dans le même sens que pseuda. ci dessus, mais qui n'est pas spécifique au suites définies par récurrence :
Une suite, effectivement, c'est jamais qu'une fonction de N->R donc c'est bien "une fonction", mais il y a une énorme différence entre les fonction de N->R et celles de R->R du fait de la différence de "nature" entre N et R.
Pour montrer un truc concernant les entiers, il suffit de la faire "de proche en proche", c'est à dire en passant d'un élément au suivant. Donc par exemple, pour montrer qu'une suite est croissante, c'est à dire en fait que Un>Um pour tout n>m, ben il suffit en fait de montrer que U(n+1)>Un pour tout n.
Par contre ce type de raisonnement ne marche évidement pas pour les fonctions de R->R vu que, lorsque l'on se donne un réel xo, y'a pas de réel "suivant de xo" (alors que n+1 est le "suivant de n" dans N).
Par contre, et à contrario, ce qui existe dans R et pas dans N, c'est qu'on peut prendre des réels x aussi proche qu'on veut de xo, c'est à dire qu'on peut faire tendre x vers xo alors que ça veut évidement rien dire dans N où on risque pas de prendre des nombres entiers qui "tendent vers 5".
Et bien sur, ce que ça permet de faire, c'est de calculer des dérivées (égale à la limite du taux de variation) qui vont plus ou moins jouer le même rôle que les U(n+1)-Un du cas des entiers pour pouvoir déterminer si une fonction de R->R est ou n'est pas croissante.
On peut même constater que le fameux U(n+1)-Un des suite, ben en fait c'est égal à (U(n+1)-Un)/((n+1)-n), c'est à dire c'est égal aux taux de variation entre n et l'entier (suivant) le plus proche de n ce qui explique en grande partie les lien qu'on a entre les deux notions (la suite (Vn) constituée Vn= U(n+1)-Un, certains auteurs l'appellent même la "dérivée discrète" de la suite (Un) )
Perso, j'aurais principalement répondu un truc qui va dans le même sens que pseuda. ci dessus, mais qui n'est pas spécifique au suites définies par récurrence :
Une suite, effectivement, c'est jamais qu'une fonction de N->R donc c'est bien "une fonction", mais il y a une énorme différence entre les fonction de N->R et celles de R->R du fait de la différence de "nature" entre N et R.
Pour montrer un truc concernant les entiers, il suffit de la faire "de proche en proche", c'est à dire en passant d'un élément au suivant. Donc par exemple, pour montrer qu'une suite est croissante, c'est à dire en fait que Un>Um pour tout n>m, ben il suffit en fait de montrer que U(n+1)>Un pour tout n.
Par contre ce type de raisonnement ne marche évidement pas pour les fonctions de R->R vu que, lorsque l'on se donne un réel xo, y'a pas de réel "suivant de xo" (alors que n+1 est le "suivant de n" dans N).
Par contre, et à contrario, ce qui existe dans R et pas dans N, c'est qu'on peut prendre des réels x aussi proche qu'on veut de xo, c'est à dire qu'on peut faire tendre x vers xo alors que ça veut évidement rien dire dans N où on risque pas de prendre des nombres entiers qui "tendent vers 5".
Et bien sur, ce que ça permet de faire, c'est de calculer des dérivées (égale à la limite du taux de variation) qui vont plus ou moins jouer le même rôle que les U(n+1)-Un du cas des entiers pour pouvoir déterminer si une fonction de R->R est ou n'est pas croissante.
On peut même constater que le fameux U(n+1)-Un des suite, ben en fait c'est égal à (U(n+1)-Un)/((n+1)-n), c'est à dire c'est égal aux taux de variation entre n et l'entier (suivant) le plus proche de n ce qui explique en grande partie les lien qu'on a entre les deux notions (la suite (Vn) constituée Vn= U(n+1)-Un, certains auteurs l'appellent même la "dérivée discrète" de la suite (Un) )
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
