Trop rapide à simplifier une intégrale?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Tilu
- Membre Naturel
- Messages: 29
- Enregistré le: 20 Fév 2017, 18:25
-
 par Tilu » 18 Mai 2017, 08:57
par Tilu » 18 Mai 2017, 08:57
Bonjour
Sujet:
Je dois intégrer un flux de densité (spectrale) vis a vis des variables de surface et d'angle solide.
L'expression du flux de densité concerné est en fonction de la longueur d'onde et de la température comme suit:

J'ai donc fait:

Et comme l'expression du flux ne dépend pas de ses deux variables, je l'ai sortie de l'intégrale pour donner:

D'où le résultat final:
 Remarque: ce qui après se simplifie car dans mon cas,
Remarque: ce qui après se simplifie car dans mon cas, 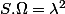
Ma question: Est ce que mon approche est correcte? Je sais que le résultat est juste mais je me demande si j'ai été un peu trop directe en sortant simplement l'expression de l'intégrale comme je l'ai fait pour n'intégrer que sur les deux variables?
Merci par avance de confirmer - ou corriger - suivant le cas.


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 18 Mai 2017, 09:45
par zygomatique » 18 Mai 2017, 09:45
salut
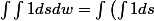dw = \int Sdw = S \int1dw = SW)
ce me semble-t-il ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Tilu
- Membre Naturel
- Messages: 29
- Enregistré le: 20 Fév 2017, 18:25
-
 par Tilu » 19 Mai 2017, 07:25
par Tilu » 19 Mai 2017, 07:25
Désolée, ça a été trop rapide pour moi. Qu'est ce qu'est le paramètre "l" dans ton intégrale? Il disparait en route pour ré-apparaitre plus loin. Pour moi, ce n'est pas évident là.

Est ce que tu pourrais expliquer plus en détail?
Merci

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 19 Mai 2017, 15:41
par zygomatique » 19 Mai 2017, 15:41
1 est la moitié de son double ....
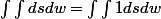
...
une fonction constante ne dépend pas de la variable ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
