Formes à reach positif

[Pierrotdu18]

Bonjour !

Je viens vous demander de l'aide sur un sujet qui n'est pas très classique et qui utilise des notions pas très courantes (enfin, il me semble).
Ainsi il faudra s'attaquer au formalisme (pas très long heureusement) que je vais vous présenter pour vraiment comprendre la question, j'espère que certains pourront me venir en aide !

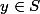
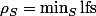
Alors, voilà : soit , on appelle plus proche voisin de à tout élément vérifiant . On appelle axe médian de l'adhérence de l'ensemble des points de qui ont au moins deux plus proches voisins dans distincts. Alors, on pose si cette définition a du sens, où est la fonction qui a un point de associe sa distance à l'axe médian de . Ce réel est alors appelé reach de .

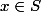
Du coup voilà ma question : si est une forme à reach strictement positif (et non infini mais en fait on s'en fiche), un document de l'école polytechnique parle des "deux disques circonscrits à en " pour un élement , en postulant sans le dire leur existence. J'essaye par tous les moyens possibles de montrer leur existence mais je n'y arrive pas, c'est pourquoi je viens vous demander de l'aide. En fait on a assez peu de contraintes sur la régularité de la forme , on sait juste qu'elle est à reach strictement positif mais on a sinon on ne sait pas à quel point elle peut être non lisse...

Néanmoins pour être honnête je ne peux pas vous cacher qu'une telle forme est alors au moins une fois différentiable, ce résultat a été montré par Federer dans son article Curvature Mesures (1959), néanmoins la démonstration utilise des outils absolument pas abordables à mon niveau (je suis un simple taupin).
Du coup je ne veux pas utiliser ce résultat.

J'espère que certains prendront le temps de réfléchir à ma question je vous remercie d'avance !
Pierre E.

[pascal16]

le S C R^d me gène, avec cette définition, j'ai l'impression que x est toujours son plus proche voisin.
S est décrite comme un partie de R^d, mais on l'appelle forme. Hors une forme et une norme, ça peut alors être une norme issue de cette forme.
Pas d'erreur dans l'énoncé ?
x, y et z sont pas dans S avec y différent de x ?

J'essaie d'appliquer à S= Z^d où j'aimerais trouver un reach de 1

[Pierrotdu18]

Aïe aïe aïe, bête erreur d'inattention... Je reformule : on appelle plus proche voisin de à tout élément vérifiant . Les autres définitions restent inchangées.
Évidemment ça change tout !

Merci déjà pour vos premières recherches

[pascal16]

Bonjour !
On appelle axe médian de l'adhérence de l'ensemble des points de qui ont au moins deux plus proches voisins dans distincts....

Du coup voilà ma question : si est une forme à reach strictement positif (et non infini mais en fait on s'en fiche), un document de l'école polytechnique parle des "deux disques circonscrits à en " pour un élement , en postulant sans le dire leur existence.

Pierre E.

Si S a un reach, elle a un axe médian, si x est sur l'axe médian, il a obligatoirement 2 plus proches voisins par définition, d'où l’existence.
A x fixé, y plus proche voisin de x, ||x-y|| te donne une boule de rayon ||x-y|| centrée sur x.
Or x a deux plus proches voisins, donc une deuxième boule concentrique (car le centre est encore x)

Revenons à aux généralité pour y voir plus clair, si j'ai bien compris :

Dans RxR, S = { (x;1/x), pour x €R*} U { (x;-1/x), pour x €R*} a un 'axe' médian, mais pas de reach (un reach = 0)
l'axe médian est l'ensemble des deux axes x=0 et y=0

Dans RxR, S= NxN, l'axe médian est NxN et le reach est 1
chaque point du plan a 4 plus proches voisins x(a;b) a pour voisin (a-1;b), (a+1;b), (a;b-1) et (a;b+1)

[Pierrotdu18]

Alors,

Je ne pense pas que ceci montre l'existence d'une quelconque boule tangente à S en x si x est dans S : on parle de x quelconque sur l'axe médian avant de parler de y son plus proche voisin dans S, ça ne peut être suffisant. Il faudrait montrer l'existence d'une boule tangente à S en x pour tout x dans S. En effet, étant donné un point x de S, il n'est pas assuré qu'il existe un point de M_S, y, tel que ||y-x|| = d(y, S).
On peut par exemple prendre un carré auquel on arrondit les coins : l'axe médian est alors composé des diagonales du carré, dont on coupe les extrémités. Alors, on dispose de pleins de points qui servent de contre exemple à beaucoup de choses qu'on pourrait penser de prime abord...

Le premier exemple est parfaitement correct, par contre le deuxième n'est pas tout à fait juste : si l'espace ambiant est R² et la forme S est N² (en fait que je dis forme je désigne un compact mais c'est pas grave ça pose pas de problème ici), l'axe médian n'est pas S, et le reach n'est pas 1...
On ne peut jamais avoir qu'une forme est égale à son axe médian, en effet tout point de S a un unique plus proche voisin qui est lui-même. Dans le cas présent, l'axe médian est (1/2,1/2) + N² et le reach est 1/2 (se voit bien avec un dessin).

[pascal16]

On ne peut pas aller plus loin sans en savoir plus sur ta source de polytechnique.
Leur définition exacte du cercle circonscrit à S en x (car si S=NxN, son rayon est infini )
Si c'est un raisonnement par l'absurde, c'est normal d'en supposer 2 au départ.
Dans ton premier post, x est dans S alors que le raisonnement semble porter sur l'axe médian.


pour le reach :
http://users.math.msu.edu/users/markiwe ... ederer.pdf
P419 : la définition du reach positif diffère dit bien l’existence d'un 'plus proche voisin' unique. Ton exercice ne serait-il pas de le démontrer ?

[Pierrotdu18]

Je connais le document de Federer bien sûr, mais il est totalement inabordable à mon niveau.
La définition que je donne du reach est équivalente, pas de soucis pour ça.

Voilà le document de l'X dont je parle : http://www.enseignement.polytechnique.fr/informatique/INF562/Notes/Poly_INF562.pdf

Le document n'est vraiment pas clair et à mon avis n'apporte rien de plus sur ces fameux disques tangents c'est pourquoi je ne l'avais pas envoyé, mais sait-on jamais.....

AJOUT : ce n'est pas un simple "exercice" de taupin, j'étudie ça dans le cadre de mon TIPE donc il n'y a pas d'énoncé prévu par un prof ni rien. C'est juste que dans le document que je viens de partager, à l'endroit "Lemme 4.4 (Disques tangents)", on parle de disques tangents à S en un point de S sans mentionner leur existence ni leur définition... Je pense que si un point est isolé dans S, on peut prendre n'importe quel disque, de toute façon le rayon n'est pas important (visiblement il doit être inférieur à d'après le document mais ce n'est pas le plus important), on ne parle pas ici d'un disque qui viendrait fitter la courbe avec le bon rayon de courbure, mais plutôt un disque ouvert dans dont le rayon peut être choisi à sa guise (tout de même assez petit pour que le disque ne rencontre pas S) tel que x soit dans son adhérence. Ainsi, il me faudrait juste montrer qu'en un point x de S, on dispose d'une boule incluse dans qui contient x dans son adhérence (et de rayon non nul). Ce sera suffisant je pense, pour que je continue toutes mes recherches tout seul. C'est ça précisément que je n'arrive pas à montrer.

[Pierrotdu18]

Désolé pour le double-post, le me permets de reformuler ma question afin de la rendre plus orientée (sans mauvais jeu de mots).

Ça va presque finir par avoir une allure d'exercice : soit une forme à reach positif. On appelle boule tangente à en toute boule où telle que et . Question : montrer qu'il existe au moins une boule tangente à en tout point .

Je suis sûr à 99.9999% que c'est vrai, sinon les chercheurs qui ont écrit le document ont des comptes à rendre La question est de savoir pourquoi...

PS : la définition de la boule tangente c'est moi qui l'ai inventée, comme le doc n'en parle pas. C'est celle qui se rapproche le plus de la réalité géométrique et topologie néanmoins et à coup sûr c'est la bonne !

[pascal16]

vu de loin :
on part d'un x quelconque, fixe de S
s'il est l'unique élément de S, S n'a pas de reach
sinon, on prend u { ||y-x||, y € S, y <> x}
u ne contient que des élements positif
le plus grand des minorants de u est donc un nombre positif (notons-le U).
mais par définition du reach, U est >= reach donc >0.
U va être le r de ta boule.
si U est atteint pour un y donné, U est en fait le minimum, c'est bon
si U n'est pas atteint pour un y donné, ça coince, c'est là que l’existence du reach impose que ce cas n'existe pas.

comme faire pour le prouver ?
utiliser la boule de rayon u+reach/2 et de centre x
cet ensemble a le même "plus grand minorant", il n'est donc pas de cardinal fini
Dans une boule, dans un univers de dimension d finie, peut-on avoir une infinité de points tous séparés d'au moins reach entre eux ?
(on s’aperçoit que la dimension finie et le reach sert dans la démo)

[Pierrotdu18]

Il me semble que la démonstration a une faille : si on considère un simple cercle dans R^2, qui est bien sûr à reach positif, si on prend x dessus, alors 0 adhère à l'ensemble u proposé... Donc U = 0 et la démonstration n'est pas correcte, en fait, la définition du reach n'est pas celle ci, on a pas nécessairement U >= reach.

[pascal16]

le cercle est continue, donc sans reach (ou reach nul), on a toujours un point aussi proche que l'on veut d'un autre point donné, aucun point du cercle n'a pas de plus proche voisin.

[Pierrotdu18]

Ah non non, le reach d'un cercle c'est son rayon. Le reach c'est le min de la lfs, comme l'axe médian d'un cercle c'est son centre seulement, la distance de tout point du cercle à l'axe médian c'est bien le rayon

[pascal16]

j'étais parti ailleurs, mais la démo va dans le bon sens.
dans ton exemple, x€S, <=> x est au centre du cercle, U= le rayon=le reach.

cas général
x€S <=> x a au moins 2 plus proches voisins <=> U= le ppe de u (et on a toujours U>= reach par définition du reach)

[Pierrotdu18]

J'imagine que S veut dire M_S plutôt, S est la forme, S son axe médian.

Je ne comprends pas trop la deuxième partie, a priori si U = lfs(x) et c est le point de l'axe médian qui minimise la distance à x, alors B(c, U) n'est pas nécessairement un bon candidat... Ou alors je n'ai pas compris.

[pascal16]

Question : montrer qu'il existe au moins une boule tangente à S en tout point x€S.

il n'y aurait pas un M_S à la fin ?

je suis désolé, il n'y a à mon avis pas besoin d'être une forme à reach pour réaliser ce que tu veux.

pour tout élément x de R^d, et E un ensemble quelconque de R^d.
x est en dehors de E, E non vide, d(x,E) existe, et ta boule a pour rayon d(x,E) et son centre est x.

par contre on n'a pas forcément d'un y € E tel que B(y,d(x,E) ) existe (si E est un ouvert par exemple).

J'arrête ici, il faut être plus clair sur les définitions et plus strict sur ce que l'on cherche.

[Pierrotdu18]

Non, pas M_S, S.

Et je suis désolé mais c'est vous qui n'avez pas compris les définitions pour le coup : je suis bien conscient qu'un tel cercle existe (celui dont vous parlez) mais ce n'est pas la définition que j'ai donnée, vous avez mal du la lire, je veux une boule qui ne contient aucun élément de S.

Si S est l'union de la droite des abscisses et de celle des ordonnées, on ne peut pas disposer d'un cercle qui touche l'origine mais qui ne continent aucun point de S. Je veux justement montrer que si S est à reach positif, c'est toujours possible.

J'espère que vous voudrez bien regarder encore un peu dans la mesure où cette fois les définitions étaient claires...

[pascal16]

pour tes deux axes.
l'axe médian est les deux diagonales privées de l'origine (c'est quoi son reach ?).
et ça sert à rien de sortir un reach car tout point x du plans en dehors des axes, il existe une boule centrée en x qui est tangente à l'un des deux axes.

En gros si tu as un ensemble E quelconque, tu le fermes, son complémentaire est un ouvert O et en tout point x d'un ouvert, il existe une boule voisinage de x qui est complètement incluse dans O et si tu fais grossir le rayon, elle 'touchera' à un moment E.

Pour que le reach serve à quelque chose, il faut que ton ensemble de départ soit composé d'éléments disjoints et en nombre infini pour ne pas tomber dans des cas qui ne servent à rien. l'axe des abscisse union NxN union un petit pavé quelque part est un minimum pour commencer à avoir des résultats intéressants.

[Pierrotdu18]

On remarque que la distance de l'origine à l'axe médian est 0 donc le reach est nul !

Et oui je suis bien d'accord sur ce point, néanmoins le problème est pris à l'envers : vous partez d'un point qui n'est pas sur la forme et vous montrez qu'on dispose d'une boule dont le centre est ce point et qui touche la forme S. Moi au contraire, partant d'un point de S, j'aimerais une boule qui touche S en ce point. Mais il ne doit pas y avoir de points de S dans la boule, du coup dans l'exemple que j'ai donné, on remarque que ce n'est pas possible partout en particulier à l'origine : il n'y a pas de boule qui touche l'origine et qui ait une intersection non vide avec S.

[pascal16]

donc une condition est que le reach soit >0.

[Pierrotdu18]

Justement, que le reach soit positif c'est la bonne condition. Mais le problème est que je n'arrive pas à le montrer. Il faudrait montrer que reach >0 ==> boule tangente en tout point mais je n'y parviens pas