Un peu de geometrie

[biss]

Salut. SVP Puis je avoir de l'aide dans cet exo de géometrie un peu compliqué a mon niveau.

On considère un cercle C et un point D extérieur au cercle. Par D, on trace une droite qui coupe C en deux points distincs A et B et une tangente au cercle C dont on note E le point de contact. On considère un point C sur AB tel que DC=DE et tel que C soit intérieur au cercle.
Montrer que la droite EC est bissectrice de l'angle AÊB.

Merci

[capitaine nuggets]

Salut !

Merci d'éviter le multi-post svp

Qu'as-tu vu en cours en rapport avec cet exercice ?

As-tu fait un dessin pour avoir des idées ?

[biss]

Oui j'ai fais un dessin et j'en est deduit que je dois montrer que AC=CB
Ou que C est le centre du centre.
Dans mon cours de geometrie plan (droite, cercle, triangle,polygone, mediatrice,bisectrice,angle...) je n'arrive pas a voir l'information qui m'aidera pour la demonstration.

[capitaine nuggets]

Attention ! Tu confonds bissectrice et médiatrice. Si 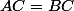alors, puisque appartient à 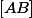, serait le milieu de [AB], ce qui n'est pas le cas en général.

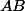Par exemple si on place et de telle manière que soit égal au diamètre du cercle 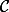et si on place assez proche de sur , est assez proche de . Donc sachant que (avec ), on peut se convaincre que .

Ce qu'il faut montrer, c'est plutôt que , ou si tu préfères .

[pascal16]

si C est sur AB EC ne peut pas être la bissectrice demandée, il y a une erreur dans la recopie de l'énoncé

[Pseuda]

Bonsoir,

Easy. D'après le th. de l'angle inscrit, on a (en vecteurs) : (DE, EB) = (AE, AB), et comme le triangle DEC est isocèle, on a une autre égalité d'angle. Il n'y a plus qu'à faire les soustractions...

[chan79]

De façon analogue
Montre que les angles bleus sont égaux ( soit )

puis que

[biss]

Merci. C'est un tout nouveau chapitre pour moi et j'arrive pas à vous suivre. Cela prouve que je dois revenir sur les differents aspects du cours et mieux les assimilés.

Chan79 : Ca parait facile de demontrer que les alphas sont egaux mais je ne vois pas comment je vais m'enslm'en sortir.

Pseuda: La deuxieme c'est (ED, EC)=(CE, CD)
Donc la soustraction fera
(DE, EB) - (ED, EC)= (AE, AB)- (CE, CD)
(ED, EC)=
La deuxieme terme me donne 1 triangle dont deux de ses angles a soustraire et je ne vois le resultat donnerai quoi.

[Pseuda]

Bonsoir,

Reprenons avec la dessin de Chan. On a :

(ED, EA) = (BE, BA) (th. de l'angle inscrit avec la tangente)
(ED, EC) = (CE, CD) (triange CDE isocèle)

par soustraction :
(EC, EA) = (BE, BA) - (CE,CD)

puis :
(EC, EA) = (BE, BA) - (pi - (CB, CE)) (angle plat)
(EC, EA) = (BE, BC) + (CB, CE)- pi = (BE, BC) + pi + (CB, CE)
(EC, EA) = (BE, CE)
(EC, EA) = (EB, EC)

[biss]

J'ai compris merci.
Une dernière question. Dans tes deux postes tu dis d'après le theorème des inscris, (ED, EA)=(BE, BA) en gros les deux angles bleus dans le schema.
Mais j'ai cherché les theoremes concernant les angles inscrits et j'en ai trouvé que deux.

Le théorème de l'angle au centre affirme que, dans un cercle, un angle au centre mesure le double d'un angle inscrit interceptant le même arc.
Le théorème de l'angle inscrit est une conséquence du précédent et stipule que deux angles inscrits interceptant le même arc de cercle sont égaux.

Mais aucune de ces deux ne permet de deduire la deduction plus en haut.

[chan79]

salut
Place E', symétrique de E par rapport au centre du cercle.
L'angle au centre (E'E,E'A) est égal à (complémentaires avec le même angle)

[Pseuda]

Bonjour,

Il s'agit du cas limite où l'angle inscrit est pris entre la corde et la tangente :

https://fr.wikipedia.org/wiki/Th%C3%A9o ... _au_centre (tout en bas)

Imagine le sommet A de l'angle (AB, AC) qui se déplace sur le cercle jusqu'à atteindre un des 2 points d'intersection B ou C.