[Arithmétique] Factorisation d'une expression

[M.Floquet]

Bonsoir, je me demandais si cette expression était factorisable : on considère deux nombres premiers impairs différents (au minimum ).

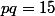
J'essaye de factoriser : .

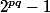
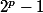
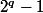
Cette expression est censée être divisible par ou mais on ne peut pas appliquer la formule de factorisation générale de la forme : où est une somme de avec non ?

Merci d'avance !

[infernaleur]

Bonsoir, pourquoi on ne pourrais pas ?
Je suis d'accord avec ta formule de factorisation

[M.Floquet]

L'hypothèse de départ change rien au final car les nombres sont fixés. J'ai essayé par exemple pour et ça coinçait...

[infernaleur]

Ah oui désoler je n'avais pas vu attentivement les hypothèses autant pour moi ^^
je ne vois pas comment factoriser (si cela est possible) j’espère qu'une personne parviendra a te répondre

[M.Floquet]

En fait ça me parait bizarre... J'ai du mal écrire mes puissances car finalement ça marche pour

[M.Floquet]

Résolu désolé...