2 boules de neiges 2 trajets
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
ortollj
- Membre Rationnel
- Messages: 554
- Enregistré le: 13 Mai 2009, 08:28
-
par ortollj » 11 Mai 2017, 19:15
Bonjour
je bute sur cet exercice
#calcul de theta
 = 0}<br />\\ \mathbf{t \; v \; \operatorname{cos} \left( theta \right) = D}<br />\\ \mathbf{t = \frac{D}{v \; \operatorname{cos} \left( theta \right)}}<br />\\ \mathbf{D^{2} \cdot \frac{g}{2 \; v^{2} \; \operatorname{cos} ^{2}\left( theta \right)} = D \; \frac{\operatorname{sin} \left( theta \right)}{\operatorname{cos} \left( theta \right)}}<br />\\ \mathbf{D^{2} \cdot \frac{g}{2 \; v^{2} \; \operatorname{cos} \left( theta \right)} = D \; \operatorname{sin} \left( theta \right)}<br />\\ \mathbf{D \; \frac{g}{2 \; v^{2}} = \operatorname{sin} \left( theta \right) \; \operatorname{cos} \left( theta \right)}<br />\\ \mathbf{\operatorname{sin} \left( theta \right) \; \operatorname{cos} \left( theta \right) = \frac{1}{2} \; \operatorname{sin} \left( 2 \; theta \right)}<br />\\ \mathbf{D \; \frac{g}{2 \; v^{2}} = \frac{1}{2} \; \operatorname{sin} \left( 2 \; theta \right)}<br />\\ \mathbf{theta = \frac{1}{2} \; \operatorname{asin} \left( D \; \frac{g}{v^{2}} \right)})
# on donne
g=9.81 m/s^2 , D=25 m , v_0=20 m/s
=0.33})
il y a quelque chose qui m'echappe, je ne trouve que le trajet le plus directe ;-(
pourtant l 'autre trajet existe je l'ai verifié avec Geogebra c'est le trajet le plus lent (celui qui monte le plus haut),on voit avec Geogebra
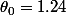
Radian (71.1 degré):
si j'avais su j'aurais pas venu.
-
Dasson2
- Membre Relatif
- Messages: 152
- Enregistré le: 24 Sep 2016, 17:00
-
par Dasson2 » 11 Mai 2017, 19:46
-
ortollj
- Membre Rationnel
- Messages: 554
- Enregistré le: 13 Mai 2009, 08:28
-
par ortollj » 12 Mai 2017, 01:55
merci Dasson2
finalement c'est super simple
 \; \operatorname{cos} \left( theta \right) = \frac{1}{2} \; \operatorname{sin} \left( 2 \; theta \right)})
le produit sin(x)*cos(x) a la meme valeur quand j'inverse les valeurs de sin et de cos !
et donc quand je trouve un angle theta je trouve aussi pi/2-theta.
ce detail m'échappait
si j'avais su j'aurais pas venu.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
