Nombre Mignon

[Drop]

Bonjour, j'ai participé récemment à un concours de niveau de seconde et je bloque encore sur la dernière question de la deuxième partie

Si vous pouviez me donner des pistes je vous serrez reconnaissant

L'énoncé est le suivant:

Problème 4.
On dit qu’un entier est mignon s’il a exactement 10 chiffres, qui appartiennent tous `a l’ensemble
{1, 2, 3}, et si deux chiffres consécutifs diffèrent systématiquement de 1.
(a) (8 points) Combien existe-t-il d’entiers mignons ?
(b) (8 points) Quelle est la somme de tous les entiers mignons ?

J'ai essayé de construire des "nombre mignon" pour trouver une relation entre eux mais je n'ai pas trouvé..


Merci de ne pas effacer des discussions une fois une réponse apportée. C'est contraire à l'esprit du forum.

[Ben314]

Salut,
Si on nombre est "mignon", à la suite d'un 2 il doit forcément y avoir un 1 ou un 3.
Par contre, la suite d'un 1 ou d'un 3, il y a forcément un 2.
Donc il y a des 2 une position sur deux et, entre deux 2, il y a au choix soit un 1 soit un 3.
Cela donne deux "types" de nombres mignons à 10 chiffres selon que le premier chiffre est un 2 ou pas.
1) Compte combien il y en a de chaque type.
2) Pour la somme, procède "colonne par colonne" en regardant combien il y en a avec un 2 dans cette position là, combien il y en a avec un 1 et combien avec un 3. Déduit en la somme totale.

[Drop]

Merci de votre réponse, mais par "si deux chiffres consécutifs diffèrent systématiquement de 1" je pensais que ça voulais dire qu'il ne peut avoir de "1" consécutif dans un nombre mignon, ok bah du coup je reprend l'éxo j'avais mal compris l'énoncé..

[Drop]

baba

[chan79]

Ok j'ai trouvé 96 "nombre mignon" en passant par du dénombrement

Salut
Pourrais-tu mettre tes calculs ? Ca me paraît beaucoup.

[pascal16]

ça donne une chaine comme ça :


96, c'est en effet un peu trop pour moi aussi
verticalement, ça me donne toujours une moyenne de 2...

[Drop]

abab

[chan79]

C'est pas "mignon" d'effacer son texte ! C'est même contraire aux usages de ce forum !

[Lostounet]

C'est pas "mignon" d'effacer son texte ! C'est même contraire aux usages de ce forum !

J'ai remis le texte d'origine et j'ai verrouillé le message ce qui empêchera toute modification.
C'est une attitude inacceptable.
Merci de respecter la charte du forum la prochaine fois.

[zygomatique]

merci ...

[chan79]

salut
Si on dessine l'arbre des solutions, il est constitué à l'aide de la séquence ci-dessous.
On arrive à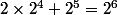
Plus généralement, avec chiffres on a si n est pair et sinon
On peut aussi nommer u(n), v(n) et w(n) le nombre de "nombres mignons" à n chiffres, se terminant respectivement par 1, 2 et 3.
On a alors:
u(n+1)=v(n)
v(n+1)=u(n)+w(n)
w(n+1)=v(n)
Juste un petit tableau à faire
Pour la question b, on trouve :

Plus généralement, si n est pair:

Pour n impair: