Limite serie entiere
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
deliche
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Fév 2017, 12:34
-
 par deliche » 23 Avr 2017, 13:31
par deliche » 23 Avr 2017, 13:31
Bonjour, j'ai f:[a,b] --->R une fonction continue. Pour tout entier naturel n>0:
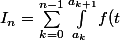 \, \mathrm{d}t)
avec

Et je dois montrer que
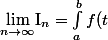 \, \mathrm{d}t)
Ca me fait penser au somme de riemman mais je sais pas trop comment m'en sortir.
Modifié en dernier par
deliche le 23 Avr 2017, 14:59, modifié 1 fois.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Avr 2017, 14:24
par Ben314 » 23 Avr 2017, 14:24
Salut,
Je comprend franchement pas le sens de la question : Pour tout n,

est trivialement égal à
dt)
(c'est la relation de Chasles pour les intégrales) et je vois pas l'intérêt d'en calculer la limite
(surtout une limite lorsque x tend vers l'infini...).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
deliche
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Fév 2017, 12:34
-
 par deliche » 23 Avr 2017, 14:59
par deliche » 23 Avr 2017, 14:59
Oui pardon c'est n qui tend vers l'infinie je rectifie mon erreur.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 23 Avr 2017, 17:19
par mehdi-128 » 23 Avr 2017, 17:19
deliche a écrit:Bonjour, j'ai f:[a,b] --->R une fonction continue. Pour tout entier naturel n>0:
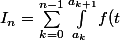 \, \mathrm{d}t)
avec

Et je dois montrer que
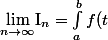 \, \mathrm{d}t)
Ca me fait penser au somme de riemman mais je sais pas trop comment m'en sortir.
Utiliser la continuité uniforme de f avec les epsilons et montrer que :
dt -(b-a)S_n(f)| < \epsilon)
où Sn(f) est une somme de Riemann
-
deliche
- Membre Naturel
- Messages: 21
- Enregistré le: 07 Fév 2017, 12:34
-
 par deliche » 23 Avr 2017, 18:42
par deliche » 23 Avr 2017, 18:42
La continuité uniforme? Mais on ne sais pas si f est uniforme.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 23 Avr 2017, 19:39
par mehdi-128 » 23 Avr 2017, 19:39
deliche a écrit:La continuité uniforme? Mais on ne sais pas si f est uniforme.
Si f est continue sur un fermé [a,b] elle est bornée d'après le théorème de Heine elle est uniformément continue sur [a,b]
 \in [a,b]^2 |x-y | \leq \eta \Rightarrow |f(x)-f(y) | \leq \frac{\epsilon}{b-a})
Ensuite essaies de montrer que il existe un N entier naturel tel que :
-f(x_k)| \leq \frac{\epsilon}{b-a})
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 23 Avr 2017, 21:17
par pascal16 » 23 Avr 2017, 21:17
Y a pas un bug d'énoncé, car comme Ben, je trouve :
Pour tout n,

est trivialement égal à
dt})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
avec