Je me présente, Laurent un étudiant en Master 2 - Recherche dans le sport. Je travaille actuellement, pour valider mon stage de fin d'étude, sur un exercice de réhabilitation suite à une blessure aux ischiojambiers. Je nécessite votre aide pour une mise en équation; je vais vous détailler tout cela, et je vous remercie du temps que vous allez investir pour lire tout ce qui va suivre!
La situation réelle, concrète c'est ça :
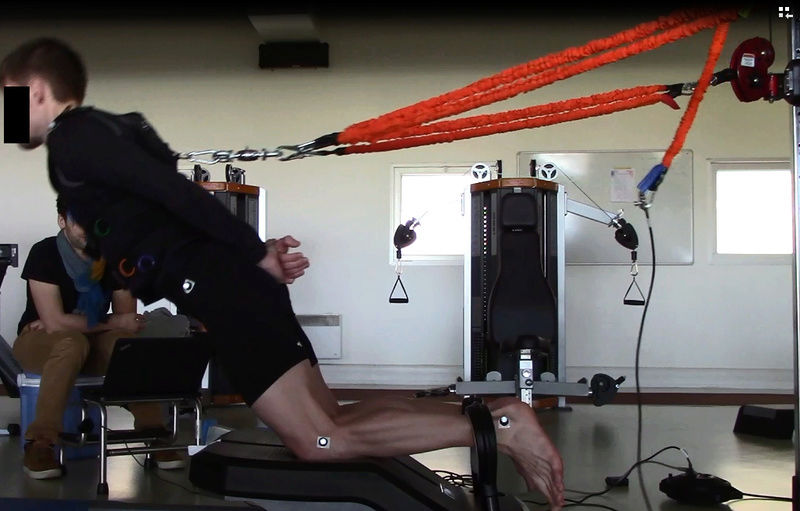
On identifie une paire d'élastique en orange, mais on va considérer qu'il n'en existe qu'un seul. Cet élastique est relié à une poulie (sur la droite de l'écran) et au harnais du sujet. On identifie une certaine distance entre l'attache du harnais et la poulie elle-même et on identifie aussi la hauteur de l'attache du harnais sur le sujet (par rapport à son genou). Enfin l'angle qui va nous intéresser est l'angle du genou (plus ou moins ouvert).
Schématiquement ça va donner ça :


Ainsi on obtient une figure avec différents paramètres d'angles et de longueurs.
Comme vous l'avez vu sur la figure le segment AB est un élastique et est donc sujet à variation en fonction de comment le sujet va se pencher. Dans le cadre de la problématique de l'expérience j'ai besoin que cette longueur ne varie pas, je m'explique.
Mon sujet A est très musclé des ischiojambiers, son angle du genou (appelons le Alpha) est très ouvert environ 140°. Cet angle correspond à l'angle maximun qu'il peut atteindre, mais bref passons, retenons que Alpha = 140°
Mon Sujet B est moins musclés, Alpha vaut chez lui 100°.
Je souhaiterai que l'assistance élastique au moment où ils atteignent leurs angles maximums soit la même. Concrètement je veux que l'élastique fournisse une assistance de 50N à 140° et à 100° mais la tension d'un élastique dépend de son élongation et forcément en fonction de l'ouverture d'angle du genou l'assistance va varier : plus le sujet va descendre bas, plus la tension/la force exercée par l'élastique sera importante.
Pour en revenir à la figure, j'ai besoin de votre aide pour formaliser une équation permettant d'avoir AB toujours de la même longueur et ceci en fonction de Alpha (l'angle du genou). La seule valeur pouvant être modifiée, ajustée c'est le segment DC. DC correspond à la distance entre le sujet et la poulie : nous pouvons l'éloigner ou bien le rapprocher.
Si c'est possible, l'équation devra prédire la distance DC en fonction de Alpha pour conserver la valeur de AB.
Concrètement, mon sujet A qui lâche à 140° sera plus proche de la poulie que mon sujet qui lâche à 100°.
Voici de manière illustrée le résumé :
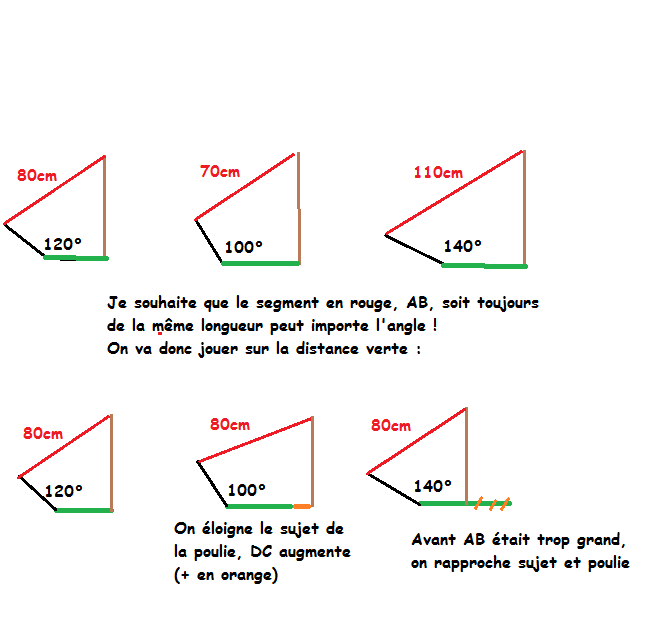
En espérant avoir été suffisamment clair ... Et ne pas vous avoir trop embrouillé avec cette histoire de tension d'élastique (il faut simplement retenir que AB doit toujours avoir la même longueur et que seul DC peut varier).
Si vous avez des questions n'hésitez pas, ce sera un plaisir d'y répondre!
Bonne journée
