Salut,
croco4 a écrit:(I) Si j'ai une suite de variables aléatoires
indépendantes _{i\geq 0})
et chaque
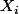
suit la loi de Bernoulli de paramètre p.
Si je regarde

, est-ce que cela veut dire que tous les
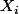
valent 1 ou que tous les
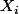
valent 0 et donc j'ai ma somme qui vaut soit 0 soit n ?
Sans même connaitre la définition
mathématique du mot "indépendant", mais uniquement avec une définition "naïve" de ce que ça signifie, a ton avis, si on avait par exemple un certain nombre de "roues de la fortune" qu'on fait tourner et que
systématiquement, toutes les roues donnent le même résultat, est ce que tu crois qu'on dirait que "ces roues sont
indépendantes les unes des autres" ou pas ?
croco4 a écrit:(II)Sauf erreur de ma part, comme je répète le procédé n fois, cela revient à utiliser une loi binomiale de paramètre (n,p) et la probabilité que ma somme, appelons la Y, soit égale à un naturel k se traduit comme:
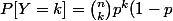^{n-k})
?[/color]
Oui, ça c'est vrai et c'est pas bien compliqué à démontrer. Et évidement, ça prouve en particulier que 'il n'y a pas (du tout) que les somme 0 et n qu'on peut obtenir comme résultat.
croco4 a écrit:Ou bien je fais fausse route et à l'intérieur de ma somme je peux très bien avoir des 1 et des 0, de sorte que ma somme ne soit pas forcément égale soit à 0 soit à n ?
Je comprend rien : le terme "ou bien", ben c'est évidement entre le laïus
(I) et le laïus
(II) qu'il fallait le mettre vu qu'il affirment deux truc totalement contradictoire l'un avec l'autre et que le
(II) te dit on ne peut plus clairement que toutes les sommes entre 0 et n (compris) sont possibles (à condition que p soit différent de 0 et de 1 bien sûr)
