Salut !
1. Ce qu'on te demande c'est si la fonction

ainsi définie est continue (sous-entendu sur

donc si tu trouves au moins un point où

n'est pas continue alors

n'est pas continue).
La courbe représentative de

te laisse bien penser que non : elle a seulement l'air continue sur tous les intervalles de la forme
\pi [)
, où

est un entier quelconque. Autrement dit, il faut montrer que

n'est pas continue en tout les point
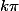
, où

est un entier quelconque. Pour cela regarde les limites de

à gauche et à droite en chaque point
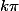
. Si elles coïncident, c'est que la fonction est continue, sinon c'est qu'elle ne l'est pas.
2. Savoir si

est dérivable n'est pas si évident que ça : il y a un peu de travail à faire. Je suis d'accord qu'il est raisonnable de dire que

est dérivable sur chaque intervalle
\pi[)
, avec

entier, mais il faut examiner ce qui ce se passe de plus près aux points
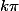
(avec

encore entier...).
Après, c'est quoi ton

?
Enfin, je te rappelle que f est de classe
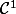
si

est dérivable et de dérivée continue.
Remarque : Du fait que

est définie sur
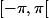
, étudier sa continuité et sa dérivabilité sur

, revient à étudier sa continuité et sa dérivabilité sur
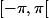
car

est supposée être

[/tex]-périodique.

