Trigonometrie

[corentinlhg]

Bien le bonjour !

je suis un peu bloquer sur une formule de trigo et j'ai besoin d'un peu d'aide pour continuer,

d'après un schema, je me suis retrouvé avec une formule que je n'arrive pas a résoudre :

A=sin(x)-sin(3x)

je cherche à isoler x et à l'exprimer en fonction de A

en utilisant le formulaire de trigonometrie je me retrouve avec : A=-2sin(x)+4sinˆ3(x)

ou en utilisant les formules d'euler je trouve : A*2i= eˆ(ix)-eˆ(-ix)-eˆ(i3x)+eˆ(-i3x)

et là je suis bloqué car je ne sais pas où aller (en fait je n'arrete pas de faire une boucle entre les trois formule quand je tente des choses)
si quelqu'un a une idée pour me mettre sur la voie ca m'aiderai bien (je ne demande pas la solution ! juste une direction pour que je trouve par moi meme)

merci d'avance !

corentin

[Ben314]

Salut,
Ben... y'a pas grand chose à dire, surtout si tu précise pas quel est l'objectif (calcul numérique ? résolution d'un exo ? autre chose ?)
De tout façon, pour trouver x, tu coupera pas à chercher tout d'abord S=sin(x) qui est (en te faisant confiance) solution de l'équation du 3em degré 4Sˆ3-2S-A=0.
Les équation du 3em degré, en théorie, y'a bien les formules de Cardan pour les résoudre, sauf qu'en pratique, ça sert à peu prés à rien : il faut souvent extraire des racines cubique de nombre complexe pour évaluer le résultat et au niveau numérique, c'est pas vraiment glop : autant y aller directement avec des trucs style méthode des tangentes de Newton pour approximer les solutions (par contre, ça peut éventuellement avoir de l'intérêt dans certains contexte théorique, mais c'est plutôt rare).

Bref, tu veut l'utiliser pour faire quoi la formule qui te donnerais le(s) x solutions en fonction de A ?

[corentinlhg]

ah oui en effet je n'ai pas donné beaucoup de détails (sorry ! )

pour x je cherche a avoir une valeur numerique une valeur d'angle plus précisement , (a etant un rapport de longueur)

x est aussi défini entre pi/4 et pi/2

j'ai une deuxième formule qui me donne a=cos(y)+cos(3y) ou cette fois ci b est compris entre 0 et pi/4
(soit y=pi/2-x)

Bon je suis un peu déçu je n'arrive pas a mettre de pièce jointe pour illustrer la formule la photo était trop volumineuses (j'essaierai de regler ça demain, il se fait tard..)

j'espère avoir été un peu plus clair, avec une illustration du problème ça sera peut-être mieux.

Bonne nuit!

[Ben314]

Si c'est pour du traitement numérique, faut pas te faire c... : tu fait le plus simple possible avec Newton.
La fonction de sur 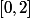est complètement adaptée à Newton donc pour un de 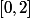donné, tu part de 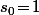puis tu itère cinq ou six fois la formule et ça te donnera le sinus du cherché avec une très très grande précision (et en très peu de temps vu la simplicité des calculs).

Par exemple, si A=0,5 tu trouve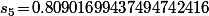 et

[corentinlhg]

bon bah super c'est ce qu'il me fallait !

je ne connaissait pas du tout la cette methode de newton, je vais me renseigner un peu dessus,
on en apprend tous les jours

merci beaucoup en tout cas tu me debloque pas mal pour le coups !

à une prochaine.

[chan79]

salut
Si on veut seulement une valeur approchée de x, geogebra la donne facilement.
Voir ci-dessous pour A=0.5