Inéquation du 2nd degré (classe de seconde)
19 messages
- Page 1 sur 1
Inéquation du 2nd degré (classe de seconde)
Bonjour, je dois effectuer un exercice dans lequel je dois résoudre l'inéquation  . J'ai essayé de factorisé à l'aide des identités remarquables ou par un facteur commun mais je n'y arrive pas après avoir fouillé sur le net il semble que les solutions soient
. J'ai essayé de factorisé à l'aide des identités remarquables ou par un facteur commun mais je n'y arrive pas après avoir fouillé sur le net il semble que les solutions soient  et
et  j'aimerais pouvoir la résoudre par calcul en comprenant la démarche. Merci de votre aide et de votre compréhension
j'aimerais pouvoir la résoudre par calcul en comprenant la démarche. Merci de votre aide et de votre compréhension
Modifié en dernier par Clementjunior le 29 Mar 2017, 18:07, modifié 1 fois.
Re: Inéquation du 2nd degré (classe de seconde)
Bonsoir,
Mettre tout à gauche, au même dénominateur :
. . . > = 0
multiplie par 3 (positif) de chaque côté de l'inégalité,
- 10x² + 100x - 150 >= 0
Quel est le signe alors du trinôme ? Et quand est-il positif pour obtenir l'intervalle-solution ? :
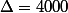
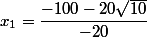 . . .
. . .
Mettre tout à gauche, au même dénominateur :
. . . > = 0
multiplie par 3 (positif) de chaque côté de l'inégalité,
- 10x² + 100x - 150 >= 0
Quel est le signe alors du trinôme ? Et quand est-il positif pour obtenir l'intervalle-solution ? :
Modifié en dernier par laetidom le 29 Mar 2017, 18:49, modifié 6 fois.
Re: Inéquation du 2nd degré (classe de seconde)
laetidom a écrit:Bonsoir,
Mettre tout à gauche, au même dénominateur :
. . . > = 0
Quel est le signe alors du numérateur ? Et quand est-il positif pour obtenir l'intervalle-solution ?
Je ne comprend pas votre, réponse lorque je ramène -50 au même dénominateur je trouve -150/3 hors que suis je sensé faire après
Re: Inéquation du 2nd degré (classe de seconde)
cours :
 à l'extérieur des racines et
à l'extérieur des racines et
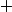 entre les racines
entre les racines
donc ta solution c'est bien entre les racines !

donc ta solution c'est bien entre les racines !

Re: Inéquation du 2nd degré (classe de seconde)
laetidom a écrit:cours :à l'extérieur des racines et
entre les racines
donc ta solution c'est bien entre les racines !
Re: Inéquation du 2nd degré (classe de seconde)
Clementjunior a écrit:laetidom a écrit:cours :à l'extérieur des racines et
entre les racines
donc ta solution c'est bien entre les racines !
Enfaite, nous n avons pas vu ce dont vous me parlez (trinome ect) donc je n ai pas le droit d'utiliser cela
Re: Inéquation du 2nd degré (classe de seconde)
Es-tu au moins d'accord avec  et tu dois savoir quand est-ce que cette quantité est positive ...?
et tu dois savoir quand est-ce que cette quantité est positive ...?
et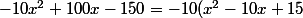)
sais-tu obtenir la forme canonique de x^2 - 10x + 15 ?
et
sais-tu obtenir la forme canonique de x^2 - 10x + 15 ?
Re: Inéquation du 2nd degré (classe de seconde)
oui je suis d accord, je dois chercher qaudn est ce que cette quantité est au dessus ou égale à 50laetidom a écrit:Es-tu au moins d'accord avecet tu dois savoir quand est-ce que cette quantité est positive ...?
et
Re: Inéquation du 2nd degré (classe de seconde)
Non, si tu es d'accord avec ce que je viens d'écrire, le 50 est passé à gauche, donc désormais on cherche quand est-ce que cette quantité est positive !
Je vais te faire un paint tu comprendras mieux, je te demande 5 minutes ! :

Je vais te faire un paint tu comprendras mieux, je te demande 5 minutes ! :

Modifié en dernier par laetidom le 29 Mar 2017, 19:41, modifié 2 fois.
Re: Inéquation du 2nd degré (classe de seconde)
Clementjunior a écrit:oui je suis d accord, je dois chercher qaudn est ce que cette quantité est au dessus ou égale à 50laetidom a écrit:Es-tu au moins d'accord avecet tu dois savoir quand est-ce que cette quantité est positive ...?
et
Non nous n 'avons pas vu encore cela
Re: Inéquation du 2nd degré (classe de seconde)
pascal16 a écrit:Au bar on commande une pinte, ici un paint.
Excellent Pascal !!!!
Re: Inéquation du 2nd degré (classe de seconde)
Si tu comprends ce paint (moins alcoolisé ! que celle du bar . . .) alors ensuite avec un tableau de signes tu peux résoudre le problème . . .
avez-vous vu la forme canonique ?
avez-vous vu la forme canonique ?
Modifié en dernier par laetidom le 29 Mar 2017, 19:45, modifié 1 fois.
Re: Inéquation du 2nd degré (classe de seconde)
laetidom a écrit:Non, si tu es d'accord avec ce que je viens d'écrire, le 50 est passé à gauche, donc désormais on cherche quand est-ce que cette quantité est positive !
Je vais te faire un paint tu comprendras mieux, je te demande 5 minutes ! :
Je comprend mieux maintenant, il suffit d'après ce que je vois de faire apparaître l'identité remarquable en rajoutant 25 de façon a convenir au double produit, c'est très gentil de votre part, merci pour votre temps
Re: Inéquation du 2nd degré (classe de seconde)
Oui, merci beaucoup.laetidom a écrit:Tu vas t'en sortir maintenant ?
Re: Inéquation du 2nd degré (classe de seconde)
Clementjunior a écrit:Oui, merci beaucoup.laetidom a écrit:Tu vas t'en sortir maintenant ?
Superbe ! Bonne soirée et @+ sur le forum !
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
