y'(1-sin(x)cos(x))+y²cosx-y+sinx=0
pourrai-je avoir la solution de cette equa diff svp
Equa diff
6 messages
- Page 1 sur 1
equa diff
par charlotttte » 26 Mar 2017, 18:53
Bonjour
y'(1-sin(x)cos(x))+y²cosx-y+sinx=0
pourrai-je avoir la solution de cette equa diff svp
y'(1-sin(x)cos(x))+y²cosx-y+sinx=0
pourrai-je avoir la solution de cette equa diff svp
Re: equa diff
par pascal16 » 26 Mar 2017, 21:38
y a pas de piste du genre chercher la solution sous la forme acos(x)+bsin(x) ?
Re: equa diff
par Ben314 » 27 Mar 2017, 03:23
Salut,
Vu le
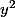
qui traine dans l'équation, je tenterais bien une homographie style 
où ça coute pas bien grand chose de supposer par exemple 
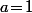
vu que 
.
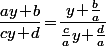
Donc on pose
qui se dérive en
(cy\!+\!d)-(y\!+\!b)(c'y\!+\!cy'\!+\!d')}{(y\!+\!d)^2}\!=\!\dfrac{(d\!-\!bc)y'\!-\!c'y^2\!+\!(b'c\!-\!bc'\!-\!d')y\!+\!(b'd\!-\!bd')}{(cy\!+\!d)^2})
Pour avoir X\cos(x)\big)y'\!+\!\cos(x)y^2\!-\!y\!+\!\sin(x)\!=\!0)
X il suffit alors de prendre \!=\!-\cos(x)\ ;\ c(x)\!=\!-\sin(x))
(mais il y a là un "petit miracle")
L'équation de départ équivaut donc à X}{1\!-\!\sin(x)y}\Big)\!=\!0)
X soit X}{1\!-\!\sin(x)y}\!=\!\lambda(\!=\!Cst))
X et au final on obtient X\!=\!\dfrac{\cos(x)\!+\!\lambda}{1\!+\!\lambda\sin(x)})
X ou bien X\!=\!\dfrac{1}{\sin(x)})
X (si 
)
Vu le
Donc on pose
Pour avoir X
L'équation de départ équivaut donc à X
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :