Démonstration de n+1 est premier

[houthor]

bonjour, j'ai 1 démonstration à effectuer assez rapidement, mais je ne vois pas comment faire, et un peu d'aide serait vraiment sympa; voici l'énoncé:
"si n est un entier naturel compris entre 1 et 7, alors si n est pair, n+1 est premier".
je sais ça à l'air bête mais en fait il faudrait surtout que je sache si je dois prouver que la contraposée est fausse (et donc la proposition sera vrai), ou est-ce que je peux démontrer pour chaque possibilité que c'est vrai?
merci d'avance!!!

[Zebulon]

Bonsoir,
oui, ici, on peut très bien essayer pour toutes les valeurs de n possibles, puisqu'il n'y en a que trois.

[houthor]

Bonsoir,
oui, ici, on peut très bien essayer pour toutes les valeurs de n possibles, puisqu'il n'y en a que trois.

merci beaucoup!!!j'espère que ce sera la bonne solution!merci encore d'avoir cherché.
bye

[Zebulon]

Je vous n prie! En réalité, je n'aime pas vraiment cette méthode, mais elle convient, même si je trouve qu'elle ne présente aucun intérêt puisqu'il s'agit d'une bête vérification.
Bonne soirée et à bientôt! :we:

[Imod]

Je ne comprend pas les réticences pour cette méthode qui , même si elle manque d'élégance est de loin la plus naturelle . Si je vous dis : montrer que dans le titre de chaque album de "tintin" il y a un "E" ( je n'ai pas vérifié si c'était vrai ) , pas d'autre démonstration que la simple étude de tous les titres .

Imod

[Zebulon]

C'est juste que c'est un hasard si ça tombe comme ça. En réalité, il n'y a rien à démontrer.

[BancH]

[CENTER][FONT=Comic Sans MS]TINTIN AU CONGO[/FONT][/CENTER]

[Imod]

Le contre-exemple qui tue :briques:

Imod

[BancH]

De plus que c'est le premier album en couleurs.

Je ne comprend pas les réticences pour cette méthode qui , même si elle manque d'élégance est de loin la plus naturelle .

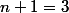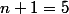ou ou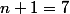

est premier, est premier, est premier donc est premier... super les maths!


Si tu veux j'ai une autre démo qui n'est pas élégante mais naturelle comme tu les aimes:

Démontrer que


On va tester cette égalité pour un très grand, si elle est recpectée, alors elle est vraie car si elle était fausse, la probabilité pour qu'elle soit vraie pour ce là seraît quasiment nulle.

On fait à la calculette

on trouve zéro, donc l'égalité est vraie.

[Imod]

Attention , je n'ai jamais dit que la méthode d'épuisement des cas était la panacée , elle est seulement extrêmement efficace quand le nombre de cas à étudier est très petit . L'idée de ton exemple si elle était juste permettrait de résoudre la conjecture de Syracuse ( qui reste ouverte ) en deux coups de cuillère à pot .

Imod

[Imod]

J'ajouterai que cette méthode qui a le don d'horrifier les étudiants s'apparente dans son principe à celle du contre-exemple qui subit les mêmes à priori :"on nous demande de démontrer que la propriété : pour tout n ... n'est pas vraie et on ne fait que qu'exhiber un exemple qui montre que ça ne marche pas . Oui mais cela suffit .

Imod

[houthor]

Attention , je n'ai jamais dit que la méthode d'épuisement des cas était la panacée , elle est seulement extrêmement efficace quand le nombre de cas à étudier est très petit . L'idée de ton exemple si elle était juste permettrait de résoudre la conjecture de Syracuse ( qui reste ouverte ) en deux coups de cuillère à pot .

Imod

merci beaucoup à tous!!!c'est sympa d'avoir cherché, et bravo d'avoir trouvé tintin au congo lol! en tout cas je vais essayer de faire ce que vous m'avez tous dit, et puis je verrais bien!
ciao merci encore!!bonne soirée