Exo dérivées + suites
16 messages
- Page 1 sur 1
exo dérivées + suites
Soit f la fonction définie sur R par f(x) = (1-2x)(e^(2x)). On note f(n) la dérivée nième de f.
1) Calculer f(n)(x) pour n = 1, 2 et 3
Pour n = 1 j'ai trouvé f '(x) = - 4x(e^(2x))
Pour n = 2 j'ai trouvé f ''(x) = (e^(2x))(-4-8x)
Pour n = 3 j'ai trouvé f(3)(x) = (e^(2x))(-16-16x)
2) Montrer par récurrence sur l'entier n non nul,que f(n)(x) = (2^n)(1-n-2x)(e^(2x))
je pars donc de f(n+1)(x) = [f(n)(x)]'
j'arrive à f(n+1)(x) = (e^(2x))(-2+(2^n)+(2^n)x2) et là je suis bloqué
Comment aller plus loin ?
3) Pour tout entier n non nul, la courbe représentative de f(n) admet une tangente honrizontale en un point Mn.
a : Calculer les coordonnées Xn et Yn de Mn. Vérifier que les points appartiennent à la courbe d'équation : y =(e^(2x))/(4^x)
b : Vérifier que la suite (Xn) est une suite arithmétique dont on donnera le premier terme et la raison. Etudier la limite de la suite (Xn).
c : Vérifier que la suite (Yn) est une suite arithmétique dont on donnera le premier terme et la raison. Etudier la limite de la suite (Yn).
Pour la 3 je bloque dès le a, je ne sais vraiment pas quoi faire !
Pourriez-vous m'aider svp ?
1) Calculer f(n)(x) pour n = 1, 2 et 3
Pour n = 1 j'ai trouvé f '(x) = - 4x(e^(2x))
Pour n = 2 j'ai trouvé f ''(x) = (e^(2x))(-4-8x)
Pour n = 3 j'ai trouvé f(3)(x) = (e^(2x))(-16-16x)
2) Montrer par récurrence sur l'entier n non nul,que f(n)(x) = (2^n)(1-n-2x)(e^(2x))
je pars donc de f(n+1)(x) = [f(n)(x)]'
j'arrive à f(n+1)(x) = (e^(2x))(-2+(2^n)+(2^n)x2) et là je suis bloqué
Comment aller plus loin ?
3) Pour tout entier n non nul, la courbe représentative de f(n) admet une tangente honrizontale en un point Mn.
a : Calculer les coordonnées Xn et Yn de Mn. Vérifier que les points appartiennent à la courbe d'équation : y =(e^(2x))/(4^x)
b : Vérifier que la suite (Xn) est une suite arithmétique dont on donnera le premier terme et la raison. Etudier la limite de la suite (Xn).
c : Vérifier que la suite (Yn) est une suite arithmétique dont on donnera le premier terme et la raison. Etudier la limite de la suite (Yn).
Pour la 3 je bloque dès le a, je ne sais vraiment pas quoi faire !
Pourriez-vous m'aider svp ?
salut,
on a:
(x)}=(2^n)(1-n-2x)e^{2x})
on note la propriété :pour n ds N*,
la propriété :pour n ds N*,(x)}=(2^n)(1-n-2x)e^{2x})
*pour n=1 je fais pas mais ça marche
*Supposons vraie pour un n#0 fixée alors par hypothèse on a:
vraie pour un n#0 fixée alors par hypothèse on a:
(x)}=(2^n)(1-n-2x)e^{2x})
regardons pour
donc ici calcule(x)}) et
et (x))^{'}})
et tu devrais pouvoir conclure
2) Montrer par récurrence sur l'entier n non nul,que f(n)(x) = (2^n)(1-n-2x)(e^(2x))
je pars donc de f(n+1)(x) = [f(n)(x)]'
j'arrive à f(n+1)(x) = (e^(2x))(-2+(2^n)+(2^n)x2) et là je suis bloqué
Comment aller plus loin ?
on a:
on note
*pour n=1 je fais pas mais ça marche
*Supposons
regardons pour
donc ici calcule
et tu devrais pouvoir conclure
Re,
on dit que la courbe de f(n) admet une tangente horizontale en um point Mn donc le coeficient directeur de la tangente est ... et l'equation de la tangente d'une courbe en un point Mn(Xn,Yn) est donnée par:
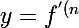(X_n)(X-X_n)+f(X_n)) donc le coefficient directeur est ...
donc le coefficient directeur est ...
bon courage
) Pour tout entier n non nul, la courbe représentative de f(n) admet une tangente honrizontale en un point Mn.
a : Calculer les coordonnées Xn et Yn de Mn. Vérifier que les points appartiennent à la courbe d'équation : y =(e^(2x))/(4^x)
on dit que la courbe de f(n) admet une tangente horizontale en um point Mn donc le coeficient directeur de la tangente est ... et l'equation de la tangente d'une courbe en un point Mn(Xn,Yn) est donnée par:
bon courage
fonfon a écrit:salut,
on a:
on notela propriété :pour n ds N*,
*pour n=1 je fais pas mais ça marche
*Supposonsvraie pour un n#0 fixée alors par hypothèse on a:
regardons pour
donc ici calculeet
et tu devrais pouvoir conclure
J'avais fait ça mais je viens de me rendre compte que j'avais fait une bête erreur de calcul ! Maintenant ça marche ! Je m'attaque à la suite !
Merci pour tes conseils !
donc c'est bon tu trouves pareil
tu calcules tu montres que ça vaut
tu montres que ça vaut  (a cste et c'est la raison)
(a cste et c'est la raison)
ensuite tu regardes ton cours pour avoir la forme de attention tu demarres à f(1)(x) et non f(0)(x)
attention tu demarres à f(1)(x) et non f(0)(x)
même principe sauf qu'il faut trouver qq chose de la forme avec q la raison et pour avoir l'expression de
avec q la raison et pour avoir l'expression de  c'est ds ton cours
c'est ds ton cours
b : Vérifier que la suite (Xn) est une suite arithmétique dont on donnera le premier terme et la raison. Etudier la limite de la suite (Xn).
tu calcules
ensuite tu regardes ton cours pour avoir la forme de
c : Vérifier que la suite (Yn) est une suite arithmétique dont on donnera le premier terme et la raison. Etudier la limite de la suite (Yn).
même principe sauf qu'il faut trouver qq chose de la forme
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
