Salut,
Deux suites
_n)
et
_n)
sont dites "équivalentes" lorsque
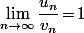
.
Et si le question est effectivement de "donner un équivalent de
_n)
" et c'est tout, alors il faut pas se faire chier et répondre "un équivalent de
_n)
c'est
_n,)
" qui est une réponse on ne peut plus correcte à la question posée. Bref, en général on pose la question "donner un équivalent
simple de
_n)
" voire même "donner un équivalent de la forme ???
_n)
".
Concernant l'exo, tout est archi. classique (mais si on l'a jamais vu, forcément c'est pas évident...) :
- On commence par "inverser la double somme" (le nombre de truc qui ... c'est jamais qu'une somme de 1) en se posant la question "à l'envers" : pour un

donné entre 1 et

, il y a combien de

pour lesquels le

en question va être un diviseur de

(donc compter "+1" dans le nombre de diviseurs de

)
- Ensuite tu obtient une nouvelle somme avec des parties entières et, évidement, tu va te dire que la partie entière de

, c'est "environ"

de façon à rendre la somme plus agréable.
Bien sur, il faut évaluer (= majorer) l'erreur commise lors de cette approximation.
- Enfin, la dernière somme que tu obtient, il faut l'approximer à l'aide d'une intégrale pour avoir une idée approximative de sa valeur et de nouveau, il faut évaluer (=majorer) l'erreur commise lors de cette approximation.
A toi de jouer.
P.S. Tu doit trouver que
_n)
est équivalent à
\big)_n)
.