Salut, comment puis je répondre à ce problème ?
Déterminer tous les p premiers tel Que le système suivant admette pour solutions (x,y) entiers
p+1=2x^2
p^2+1=2y^2
Merci d avance
Système Avec Premiers
7 messages
- Page 1 sur 1
Re: Système Avec Premiers
salut
pas le bon forum
donc (p + 1)^2 = 4x^4
donc 2p = 4x^4 - 2y^2 <=> p = 2x^4 - y^2
...
pas le bon forum
donc (p + 1)^2 = 4x^4
donc 2p = 4x^4 - 2y^2 <=> p = 2x^4 - y^2
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Système Avec Premiers
Salut
Je dis peut être une bêtise mais je crois avoir deja étudié cet exo (tiré d une compétition allemande) et De mémoire la reponse était p=7. (Ce qui fonctionne bel et bien avec la formule De zygomatique).
Reste à prouver que 7 est l unique solution.
Je dis peut être une bêtise mais je crois avoir deja étudié cet exo (tiré d une compétition allemande) et De mémoire la reponse était p=7. (Ce qui fonctionne bel et bien avec la formule De zygomatique).
Reste à prouver que 7 est l unique solution.
Re: Système Avec Premiers
merci de vos reponses !
D'accord mzis je peux prouver comment que 7 est l'unique solution svp ?
D'accord mzis je peux prouver comment que 7 est l'unique solution svp ?
Re: Système Avec Premiers
Salut,
On a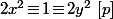 et
et 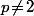 donc
donc (x\!+\!y)\!\equiv\!0\ [p]) c'est à dire
c'est à dire ) .
.
Vu l'énoncé on peut supposer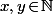 et dans ce cas on a clairement
et dans ce cas on a clairement 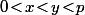 ce qui signifie que la seule possibilité pour que
ce qui signifie que la seule possibilité pour que ) soit vérifiée est
soit vérifiée est 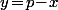 .
.
D'où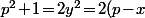^2\!=\!2p^2\!-\!4px\!+\!2x^2\!=\!2p^2\!-\!4px\!+\!p\!+\!1) donc
donc 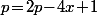 c.a.d.
c.a.d. 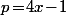 .
.
Enfin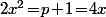 donc
donc 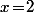 ,
, 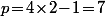 et
et 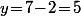 .
.
On a
Vu l'énoncé on peut supposer
D'où
Enfin
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Système Avec Premiers
p.. (j'suis) trop con ... même pas pensé à travailler modulo p ...
merci ben !!
merci ben !!
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
