Transformation de Möbius

[CoupalLee]

Bonjour,

J'ai de la difficulté avec les transformations de Möbius,

Soit : Trouver un transformation de Möbius telle que l'image de Re(z) + 1 ≥ Im(z) est Re(z) ≥ -1

Merci,

[Ben314]

Salut,
Une homographie (ou transformation de Möbius si tu veut), c'est de la forme avec , .
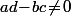Ca envoie les cercles / droites sur des cercles / droites ainsi que les "demi espaces" de frontière de cercle/droites (i.e. demi plan, intérieur de disque, extérieur de disque) sur des ensemble de "même nature".
Là, pour faire des calculs, je pense que c'est plus simple de commencer par raisonner avec des égalités, c'est à dire en disant que la droite Re(z) + 1 = Im(z) doit être envoyé sur la droite Re(z) = -1 ce qui signifie que, pour tout x réel, tu doit avoir Ré=-1 et c'est ça que tu doit résoudre (i.e. chercher a,b,c,d).
Aprés, il restera à regarder dans quel cas les demi plans correspondants sont bien envoyés l'un sur l'autre.

[CoupalLee]

Merci du coup de main !