Intégrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
kamena
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Fév 2017, 19:26
-
 par kamena » 28 Fév 2017, 01:05
par kamena » 28 Fév 2017, 01:05
j'ai besoin d'aide pour l'exercice suivant que j'ai cherché en vain :
Soit f la fonction définie par
=2x+1-xe^{x-1})
a) montrer que
=0)
admet une solution

.
b)calculer à l'aide de l'intégration par partie
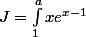
c) calculer l'aire du plan limité par la courbe cf l'axe des abscisses et les droites d'équations
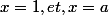
.
d)montre que l'aire
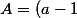(a+1/2))
.
en a) après avoir étudié les variations de f j'ai utilisé le théorème des valeurs intermédiaires . mais la suite me pose problème .merci d'avance !
-
kamena
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Fév 2017, 19:26
-
 par kamena » 28 Fév 2017, 01:24
par kamena » 28 Fév 2017, 01:24
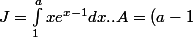(a-1/2))
.
excuse -moi.
-
aviateur
 par aviateur » 28 Fév 2017, 02:49
par aviateur » 28 Fév 2017, 02:49
L'indication est ds la question: on fait une i.p.p.
C'est à dire (je ne mets pas les bornes)
une "i.p.p." correspond à la formule
 g'(x) dx= f(x) g(x)-\int f'(x) g(x) dx.)
Dans votre cas si vous choisissez f(x)=x, votre intégrale va être remplacée (via cette formule) par une intégrale
ou f(x) est remplacée par f'(x)=1. La nouvelle intégrale ayant toute les chances d'être + facile à calculer.
Essayez.
Par contre la question D me semble bizarre.
-
kamena
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Fév 2017, 19:26
-
 par kamena » 28 Fév 2017, 14:21
par kamena » 28 Fév 2017, 14:21
en b ) j'ai eu le résultat suivant :

. est-ce juste ? et la suite comment faire ?
-
aviateur
 par aviateur » 28 Fév 2017, 15:20
par aviateur » 28 Fév 2017, 15:20
Bonjour, Non, je ne crois pas que c'est juste mais pour en être sûr :
1. D'abord il faut d'abord refaire tes calculs et (ou) me donner les détails pour voir si il y a bien une erreur.
2. De toute façon pour la suite, l'idée est de retenir que a est solution d'une équation et donc on a une relation entre a et exp(a-1), ce qui permet d'éliminer exp(a-1) ds l'expression de A qui à mon avis me semble incorrect.
Mais je le redit il faut les calculs pour que je "pointe " les erreurs.
-
Tiruxa47
- Membre Relatif
- Messages: 343
- Enregistré le: 14 Jan 2017, 16:03
-
 par Tiruxa47 » 28 Fév 2017, 17:33
par Tiruxa47 » 28 Fév 2017, 17:33
kamena a écrit: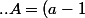(a-1/2))
.
excuse -moi.
Bonjour,
D'après moi il faut trouver
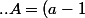(a-\frac{1}{a}))
-
aviateur
 par aviateur » 28 Fév 2017, 18:34
par aviateur » 28 Fév 2017, 18:34
Oui , c'est possible. mais avant tout il faut voir le résultat de la question 1
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 01 Mar 2017, 11:27
par siger » 01 Mar 2017, 11:27
bonjour
lorsque l'on cherche a encadrer une racine d'une equation f(x) = 0 entre deux valeurs p et q il faut montrer que f(p) et f(q) sont de signe opposés (la courbe coupe l'axe des x entre p et q)
en general on montre que f(p)*f(q) <0
ici il est plus simple de montrer que f(2) est negatif et f(1,9) positif
int (x*(e^x)dx = (x-1) e^x
d'ou
J=(a-1)e^(a-1)
mais 2a+1-a*e^(a-1)=0 par definition de a
d'ou e^(a-1)= 2+1/a
J= (a-1)(2+1/a)
A= int(de 1 à a) f(x) = a²-1+a-1- J
.........
-
aviateur
 par aviateur » 01 Mar 2017, 15:38
par aviateur » 01 Mar 2017, 15:38
Bonjour d'accord pour les résultats.
Pour l'encadrement de, il faut effectivement qu'il y ait un changement de signe;i.e f(2) est négatif et f(1,9) positif .
Mais derrière cela il y a le th des valeurs intermédiaires pour montrer l'existence de cette racine et puis il y a le pb de l'unicité. En effet rien ne dit qu'il y une seule racine entre 1.9 et 2.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
