Expression de l'espérance

[capitaine nuggets]

Bonjour, j'ai vu qu'il était possible de définir l'espérance d'une variable aléatoire , d'un certain espace probabilisé dans l'espace mesurable , intégrable et qui admet une fonction de répartition , par :

.

Cependant, j'aimerais savoir si le fait que admette une fonction de répartition implique que admet alors une densité de probabilité ?

En admettant cela, j'aimerais donc bien montrer qu'effectivement, on a bien :



(et ce, sans passer par la définition version théorie de la mesure de l'espérance : ).

Pour cela, je procède ainsi :



Donc :



Je cherche à vouloir utiliser le théorème de Fubini donc pour cela, j'écris que . On a alors :





Or pour , donc finalement, j'en déduis que :


Je ne comprends donc pas pourquoi je ne retrouve pas le résultat escompté...
Merci d'avance pour votre aide

[Matt_01]

Tu pourrais écrire cette égalité si X est positive. Si X est quelconque, c'est facilement visible que c'est faux en général, vu qu'on a aucune raison de connaître l'espérance de X si on connait juste son comportement (ie sa fonction de répartition) que pour les valeurs positives.

[Ben314]

Salut,
Je comprend franchement pas ce que tu bricole.
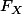
Déjà le début, je comprend pas bien ce qui peut te passer par la tête avec des trucs du style "... en supposant que ma v.a.r admet une fonction de répartition ". Pour toi, c'est quoi la définition d'une "fonction de répartition" pour une v.a.r. ? Et dans quel cas ça pourrait ne pas exister ?

Idem (voire pire...) concernant

Cependant, j'aimerais savoir si le fait que admette une fonction de répartition implique que admet alors une densité de probabilité ?

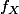
C'est quoi pour toi la définition d'une "densité de probabilité" ?
Et par exemple si on prend comme v.a.r. le résultat d'un jet de dès, tu crois vraiment qu'il y a une densité ?
Et il me semble pas que ce soit un exemple "complètement capilotracté" de v.a.r., non ?

Enfin ça

.

Je sais pas d'où tu le sort, mais c'est archi trivialement... complètement faux : comment veut tu calculer l'espérance d'une v.a.r. en ne tenant aucun compte des valeur négatives que prend ta v.a.r. ?
Parce que ta formule, en particulier ce qu'elle dit, c'est que si une v.a.r. ne prend que des valeurs négatives (i.e. ) alors son espérance est forcément nulle. Ca te semble crédible toi ?

Par contre, c'est effectivement crédible (et en fait c'est vrai) si au contraire ta v.a.r. ne prend que des valeurs positives, (i.e. ). Et dans le cas particulier où ta v.a.r. est "à densité" alors ça peut éventuellement se montrer comme tu le fait, mais c'est évidement des intégrales de 0 à +oo absolument partout.

EDIT : J'avais pas vu le message de Matt_01...

[capitaine nuggets]

Ah ok, c'est une hypothèse que je n'avais pas : que X soit à valeurs positives.