Diagonalisation par bloc

[allmess]

Bonsoir,

Est il vrai qu'une matrice symétrique par bloc est diagonalisable par bloc ?
Et si oui, y a t il une méthode pour la diagonaliser en ne travaillant qu'avec les blocs ?

Merci d'avance !

[samoufar]

Bonsoir,

La matrice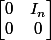 (où est la matrice identité d'ordre ) est-elle symétrique par blocs ? Est-elle diagonalisable ?

[Ben314]

Salut,
A mon sens, tout le problème est de savoir ce que tu entend par "symétrique par bloc" et ce que tu entend par "diagonalisable par bloc".
Autant le premier (symétrique par bloc), j'entrevois quelques définitions possibles et le fait que de telles matrices vont être ou non diagonalisable (tout court) va dépendre de la définition qu'on prend. (*)
Autant le second (diagonalisable par bloc), je vois même pas une quelconque définition plausible...

EDIT : (*) Encore que, les définitions "plausibles" que je vois de "symétrique par bloc" et qui produisent effectivement des matrices systématiquement diagonalisable, ben en fait elle sont aussi "symétrique tout court" donc ça a franchement aucun intérêt comme définition.

[allmess]

Merci pour vos réponses!

Ok, désolé, mes termes étaient vraiment hasardeux.

Ce que je voulais dire, c'est, si on a une matrice de la forme , peut on toujours la mettre sous la forme (de la même manière qu'une matrice symétrique est diagonalisable).

Merci d'avance !

[allmess]

Ok, la réponse doit donc être non.
Mais dans ton exemple, la matrice est alors déjà sous la forme recherché.

Merci pour ta réponse !

[Ben314]

La définition me semble un peu bizarre du fait que les matrice 2x2 symétriques, c'est celle de la forme avec 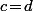mais pas forcément 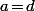, mais vu que c'est juste une nouvelle définition, ben... pourquoi pas...

Et sinon, ben je vois pas de raison particulières que ce soit vrai, en particulier tu risque pas du tout d'adapter la preuve classique concernant les vraies matrices symétriques, mais d'un autre coté y'a non plus pas de contre exemple qui me "saute aux yeux".
Enfin, pour ce type de truc, exactement comme pour le théorème concernant les matrices symétrique usuelles (et contrairement à d'autres résultats), ben faut faire gaffe au fait que ça risque de dépendre du corps de base sur lequel on se place : corps fini, Q , R , C , . . . Par exemple une matrice symétrique à coeff. dans Q, ben tu peut pas la diagonaliser dans Q.
Donc pour chercher des contre exemples (éventuels), il faudrait peut être "cadrer" le truc en précisant sur quel corps ça t'intéresse d'avoir (ou pas) le résultat.

Mais dans ton exemple, la matrice est alors déjà sous la forme recherché.

Oui : j'ai mal compris la question au départ et j'ai enlevé mon post (visiblement juste avant que tu poste le tien...)