Dérivé 1ereS

[xsylv1z]

Bonjour !
j'aimerai savoir si quelqu'un peu me donné une piste car je bloque totalement...
Il faut écrire la dérivé de la fonction suivant :

Mais sous la forme avec un réel.
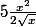
J'ai réussi à arrivé à la forme de base, mais je ne vois pas le chemin a prendre pour arriver a trouver la forme demander...
Merci !

[Pseuda]

Bonjour,

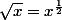
Soit tu sais que , car tu sais que : , et il suffit d'additionner les exposants,
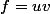
Soit, en utilisant les théorèmes concernant la dérivation des fonctions, tu poses : , avec et et tu dérives comme la dérivée du produit de 2 fonctions.

[xsylv1z]

bah oui c'est ce que j'ai fais justement, c'est en faisant ça qu'on arrive au résultat de base que j'ai donné, mais il faut le modifier pour arrivé a la forme demandé

[WillyCagnes]

bjr

F(x) =x²Vx

tu poses U=x²
V=racine(x)

U'=2x
V'=1/2racine(x)
(UV)'=U'V+V'U et tu fais le calcul, puis en simplifiant tu devrais trouver (5/2) x racine(x)
de la forme K x racine(x)

rappel 1/Vx=Vx/x

[xsylv1z]

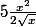
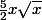
Mais comment en partant de tu arrive à ? Oo

[Pseuda]

Ah d'accord, je n'étais pas sûre d'avoir bien compris la question.

= = = (car )

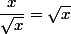
[xsylv1z]

ah non attend je crois avoir trouvé !
merci !

[xsylv1z]

merci tu a confirmé mes calculs !