Suite complexe

[Flucked]

Bonjour,

Z0=2 et Zn+1=(1+i)/2 * Zn

An le point d'affixe Zn

Montrer que O An A(n+1) est un triangle isocèle rectangle.

D'après mon dessin il est rectangle isocèle en Z(n+1) J'ai calculé la forme exp de Z(n+1) et je trouve



Mais je ne sais pas quoi faire apres

Merci

[Tiruxa47]

Bonjour,

Ecrire l'égalité des modules puis celle de arguments à partir de Zn+1=(1+i)/2 * Zn

Les arguments vont donner l'angle de sommet O du triangle étudié.

Les arguments donnent une relation entre OAn et OAn+1

On peut aussi éventuellement calculer An+1An en calculant le module de zn+1 - zn

[Flucked]

Pour donner plus de détail j'avais aussi montré que


Et que


Je fais quoi avec l'angle O ? il me faut l'angle An+1

Merci

[Pseuda]

Pour donner plus de détail j'avais aussi montré que


Et que


Je fais quoi avec l'angle O ? il me faut l'angle An+1

Merci

Bonjour,

J'ai rectifié Zn en Zn+1 dans ton module.

= mesure de l'angle

[Flucked]

Ok merci !

pour montrer qu'il est isocèle:

[Pseuda]

Il est donc rectangle isocèle en .

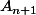
[Flucked]

merci bcp