Asymptote oblique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
stef78
- Membre Relatif
- Messages: 142
- Enregistré le: 18 Mai 2006, 16:57
-
par stef78 » 16 Oct 2006, 20:44
Bnjr on a:
= \frac{x^3+10x}{x^2+1})
Il me demande de calculer la lim en +oo et -oo
pour +oo je trouve +oo et pour -oo je trouve -oo
il me demande ensuite de demontrez que la courbe C representant f dans un repere a une asymptote oblique delta au voisinage de
oo et -oo
or je sais que pour que C ait une asymptot oblique il faut que:
Lim +-oo [f(x) - (ax+b)]= 0
or je vois pas comment appliquer ca ici pouvez vous m'aider?
-
smaths
- Membre Naturel
- Messages: 35
- Enregistré le: 21 Juin 2006, 19:45
-
par smaths » 16 Oct 2006, 22:33
Bonjour
Formule pour calculer
s'il existe :
}{x})
Si
est un nombre fini on calcule
:
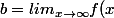 - ax)
Si
est un nombre fini alors une équation de l'asymptote oblique en l'infini à la courbe représentant la fonction
est :
.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
par Imod » 17 Oct 2006, 13:11
On peut aussi remarquer que :
=\frac{x(x^2+1)+9x}{x^2+1}= x + \frac{9x}{x^2+1}})
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
