Ne pas oublier que les lignes de
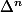
, c'est bêtement les coeff. barycentrique qui vont apparaitre à la n-ième étape.
Dire que
le diamètre tend vers 0, ça signifie que tout les points tendent vers le même point donc que toute les lignes de
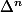
tendent vers les mêmes valeurs (par construction les sommes de lignes valent 1) donc que
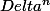tend vers une matrice de rang 1 et en cogitant un peu au niveau algèbre linéaire, ça signifie que toutes les v.p. sont de module <1 sauf une qui est égale à 1 et dont le s.e.v. propre est de dim 1.
Le même type de raisonnement montre que, si
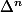
tendait vers une matrice de rang 2, ça signifierais que les coeff. "finaux" apparaissant sont dans un s.e.v. de dim 2 et que les points "finaux" sont tous alignés sur une même droite quelque soit la position de ceux de départ (on peut parfaitement considérer que les p points de départ vivent dans un espace affine de dimension aussi grande qu'on veut : ça ne change rien au processus).
Etc, etc...
Et en fait, le nombre de v.p. de module 1 et la taille des s.e.v. propre associés te donne en fait bien plus d'information que de savoir si le diamètre tend ou pas vers 0 : éjà, ça te dit si le processus converge ou pas (il faut et il suffit que 1 soit la seule v.p. de module =1) et si ça converge, ça te donne la dimension du s.e.affine dans lequel va être ton polygone "limite" (il faut regarder la dimension du s.e.v. associé à la v.p. 1)
)
!
