Salut,
Y'a pas de méthode bien bien redoutable qui marcherais à tout les coups, mais dans un cas pareil, c'est pas la mer a boire non plus.
Le cardinal de S4, c'est 4!=24 donc tu cherche un sous groupe d'ordre 8 donc ne contenant que des éléments d'ordre 1,2,4 ou 8.
L'ordre 8, c'est exclu, y'en a pas dans S4.
L'ordre 4, y'en a, par exemple a=(1234) qui engendre donc un groupe H d'ordre 4 (et y'a rien à "vérifier").
Sauf qu'y faudrait y rajouter autre chose pour passer à l'ordre 8.
Mettons qu'on rajoute un certain b (qui ne soit évidement pas dans H).
Les éléments
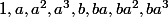
sont évidement distincts (sinon b serait dans H) donc si on veut pas dépasser l'ordre 8, c'est qu'on a tout le monde et en particulier, ça veut dire que

doit être un des éléments de cette liste et comme ça ne peut pas être un
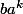
c'est qu'on doit avoir
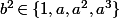
.
On peut pas avoir
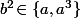
vu que ça signifierais que

est d'ordre 8 donc

.
De même,
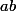
doit être dans la liste et en fait
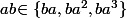
, c'est à dire
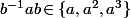
.
Arrivé à ce stade, on peut faire un peu plus de théorie ou bien commencer à procéder à des essais :
- Si b=(12) alors
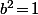
mais
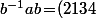)
(*) n'est pas un
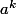
.
- Si b=(13) alors
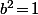
et
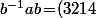\!=\!a^3)
: BINGO
On considère donc le groupe engendré par a=(1234) et b=(13). Il contient évidement les 8 éléments cités çi dessus et il ne contient bien que ceux là et rien d'autre (**) vu que la "règle"
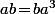
permet "d'échanger" les

et les

et donc permet de mettre le(s)

au début.
Par exemple le produit de

et de
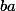
est
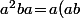a\!=\!a(ba^3)a\!=\!(ab)a^4\!=\!(ba^3)a^4\!=\!ba^7\!=\!ba^3)
.
Bref, le bilan, c'est (comme souvent) d'éviter de trop se "salir les mains" en redescendant au niveau de l'écriture des permutations pour plutôt se concentrer sur la structure de groupe même, c'est à dire sur la façon dont les éléments du groupe "se combinent".
(*) C'est pas con de savoir comment sa marche les conjugués des permutations : (12) échange 1 et 2 donc si on conjugue (1234) par (12) ça donne (2134)
(**) i.e. l'ensemble des 8 éléments cités forme bien un groupe.

