Problème sur un calcul apparement simple

[jonathan31400]

Bonjour, premier post sur ce forum donc merci à tous pour l'initiative du site !

Je suis post Bac ( bts sio 1er année ) mais j'ai trouvé intéressant de mettre ce post ici car c'est du programme de 1ère/terminale S.

Ma leçon est donc sur les suites.

J'étudie les variations de suite, on m'apprend d'abord à étudier la variation d'une suite avec Un+1 > Un
Ensuite j'arrive au niveau ou on me dit que la variation d'une suite à termes strictement positifs peut être calculé avec ceci:

Un+1 >= Un <=> (Un+1)/(Un) >= 1

et

Un+1 <= Un <=> (Un+1)/(Un) <= 1

L'étude des variations de u revient alors à comparer (Un+1)/(Un) à .

La définition est comprise, mais j'arrive à ce calcul que je ne comprends pas dans l'exemple qui suit la définition:


La suite (Un)n définie sur N par: Un = 1 / ( n(n+1) ) est une suite à termes strictement positifs.

(Un+1) / ( Un ) = (1/ (n+1)(n+2) ) / ( 1/ n(n+1) ) = n(n+1) / (n+1)(n+2) = n / (n+2)

C'est un peu brouillon, mais je ne sais pas comment afficher des barre de fraction sur le forum..( voir screen )
Je n'arrive donc pas à savoir comment on passe de la première étape à la seconde, et encore moins de la seconde à la troisième étape.

Malgré ceci, je comprend très bien que n/(n+2) <= 1


Je vous met un screen de ma leçon au cas ou, ce sera bien plus lisible.

En espérant une réponse rapide,

Très cordialement, Jonathan

[laetidom]

Bonjour,



diviser c'est multiplier par l'inverse !

simplification par (n+1) commun en haut et en bas (car on a que des produits !)

et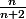 est forcément strictement plus petit que 1 puisque l'on divise quelque chose (n) par une quantité un peu plus grande (n+2),
par ex, divise 10/(10+2) = 10/12 = 0.83...., ou 101/103 = 0.98...., etc. c'est toujours < 1.




". . . je ne sais pas comment afficher des barre de fraction sur le forum . . . "
Pour info, pour bien écrire : guide-utilisation-f41/ecrire-des-belles-formules-mathematiques-balises-tex-t70548.html

Bonne journée.

[zygomatique]

salut

cours de collège :

diviser par un nombre c'est multiplier par son inverse

règle fondamental des fractions :