Déjà, je suis pas très certain que ce soit malin de raisonner en terme de minima/maxima locaux lorsque l'on fait de l'arithmétique sur les polynômes, surtout à coefficients dans Z. Et en plus, je vois franchement aucune raison qu'ils aient n-2 minimum/maximum locaux.
Tu peut expliquer quel raisonnement te conduit à ce résultat ?
A mon avis, la bonne façon de poursuivre, c'est de dire que
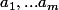
sont racines (distinctes) de
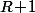
et que
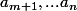
sont racines (distinctes) de
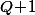
.
Or,
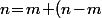\leq d^o(R\!+\!1)\!+\!d^o(Q\!+\!1)\!=\!d^o(R)\!+\!d^o(Q)\!=\!d^o(P)\!=\!n)
donc en fait
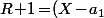...(X\!-\!a_m))
et
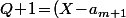...(X\!-\!a_n))
et on a donc
...(X\!-\!a_n)\!-\!1=P=RQ=\!\Big((X\!-\!a_1)...(X\!-\!a_m)\!-\!1\Big)\Big((X\!-\!a_{m+1})...(X\!-\!a_n)\!-\!1\Big))
Et on en déduit en développant le terme de droite et en simplifiant que
...(X\!-\!a_m)+(X\!-\!a_{m+1})...(X\!-\!a_n)=2)
Ce qui est clairement impossible pour des raisons de degré.