
DM de maths niveau première S
7 messages
- Page 1 sur 1
DM de maths niveau première S
Bonjour à tous, j'espère que vous avez tous passé un très joyeux noël et je vous souhaite des excellentes fêtes pour le nouvel an à venir ainsi qu'une très bonne rentrée. Je suis en première S européenne et je rencontre actuellement des difficultés dans le Devoir Maison que le professeur de mathématiques nous a octroyé. J'aimerais que vous puissiez me venir en aide s'il vous plait ce serait très sympathique de votre part.


Re: DM de maths niveau première S
Salut Noragami et bienvenue,
Cet exercice est un peu plus théorique que les autres mais les idées sous-jacentes ne sont pas difficiles.
Par exemple on peut commencer par la 1).
On sait que l'écart-type est un nombre positif qui est la racine de la variance V par définition, ou bien
est un nombre positif qui est la racine de la variance V par définition, ou bien  si tu préfères.
si tu préfères.
Habituellement pour calculer la variance de la série statistique on applique la formule du cours, qui est:
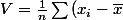^2})
Le symbole sigma indique que l'on fait la somme sur toutes les valeurs de la série statistique (que la valeur
de la série statistique (que la valeur appartienne à l'intervalle I ou pas, peu importe!)
appartienne à l'intervalle I ou pas, peu importe!)
Or l'astuce consiste à se dire qu'une valeur donnée soit appartient à I soit n'appartient pas à I donc finalement le calcul de la variance (qui est le carré de sigma) se ramène à (en multipliant par n les deux membres)
donnée soit appartient à I soit n'appartient pas à I donc finalement le calcul de la variance (qui est le carré de sigma) se ramène à (en multipliant par n les deux membres)
^2} + \sum_{i \notin I}^{}{(x_i - \bar{x})^2} = n \sigma^2 = nV)
Or la première sommede gauche est une somme de nombres positifs, et si on enlève cette somme de gauche on obtient forcément un résultat plus petit, ie:
^2} \leq \sum_{i \in I}^{}{(x_i - \bar{x})^2} + \sum_{i \notin I}^{}{(x_i - \bar{x})^2} = n\sigma^2)
Cet exercice est un peu plus théorique que les autres mais les idées sous-jacentes ne sont pas difficiles.
Par exemple on peut commencer par la 1).
On sait que l'écart-type
Habituellement pour calculer la variance de la série statistique on applique la formule du cours, qui est:
Le symbole sigma indique que l'on fait la somme sur toutes les valeurs
Or l'astuce consiste à se dire qu'une valeur
Or la première sommede gauche est une somme de nombres positifs, et si on enlève cette somme de gauche on obtient forcément un résultat plus petit, ie:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de maths niveau première S
Merci de votre réponse c'est très gentil mais pourriez vous approfondir un peu plus s'il vous plaît car je n'ai pas tout compris. 
Re: DM de maths niveau première S
Je ne vois pas comment détailler plus que je ne l'ai fait...
Donc tu pourrais peut-être relire mon post et dire précisément ce que tu ne comprends pas.
Donc tu pourrais peut-être relire mon post et dire précisément ce que tu ne comprends pas.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de maths niveau première S
Je suis désolée,
"Or l'astuce consiste à se dire qu'une valeur donnée soit appartient à I soit n'appartient pas à I donc finalement le calcul de la variance (qui est le carré de sigma) se ramène à (en multipliant par n les deux membres)"
"
Or la première sommede gauche est une somme de nombres positifs, et si on enlève cette somme de gauche on obtient forcément un résultat plus petit, ie:
"
C'est ça que je n'ai pas compris.
Pouvez vous me venir en aide pour la suite quand j'aurais compris s'il vous plait
"Or l'astuce consiste à se dire qu'une valeur donnée soit appartient à I soit n'appartient pas à I donc finalement le calcul de la variance (qui est le carré de sigma) se ramène à (en multipliant par n les deux membres)"
"
Or la première sommede gauche est une somme de nombres positifs, et si on enlève cette somme de gauche on obtient forcément un résultat plus petit, ie:
"
C'est ça que je n'ai pas compris.
Pouvez vous me venir en aide pour la suite quand j'aurais compris s'il vous plait
Re: DM de maths niveau première S
Si tu considères un intervalle I = [2 ; 10] par exemple et que tu as une série statistique x1 = 1
x2 = 1.5
x3=3
x4=5
x5 = 12
Alors pour calculer la variance tu prends chacune de ces valeurs x1, x2, x3, x4 et x5, tu calcules la variance (pour tous les x_i). Parmi ces xi il y en a qui sont dans l'intervalle I = [2 ; 10] et il y en a qui ne le sont pas.
x2 = 1.5
x3=3
x4=5
x5 = 12
Alors pour calculer la variance tu prends chacune de ces valeurs x1, x2, x3, x4 et x5, tu calcules la variance (pour tous les x_i). Parmi ces xi il y en a qui sont dans l'intervalle I = [2 ; 10] et il y en a qui ne le sont pas.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de maths niveau première S
D'accord, merci beaucoup. Comment procéder aux questions suivantes svp
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
