Condition nécessaire de CV d'une intégrale

[flashnext]

Bonjour à tous !

Si une fonction f continue sur [a, + l'infini[ (a réel) admet une limite en l'infini et que celle-ci est non nulle, alors l'intégrale de a à l'infini de f(x)dx diverge.
Certes "ça se voit", mais est-ce quelqu'un aurait une démonstration bien propre svp ? Je n'en trouve pas sur le net.

Merci ! Bonnes vacances

[Lostounet]

Pourquoi dis-tu limite non nulle?
1/t est continue si a>0 de limite nulle. Et pourtant!

Edit: tu as bien précisé condition nécessaire! Désolé :p

[flashnext]

Certes il y a aussi des fonctions dont la limite en l'infini est nulle et dont l'intégrale de a à l'infini DV.
Mais ce que j'essaie de démontrer, c'est : lorsque f admet une limite l en l'infini , alors une condition nécessaire (non suffisante !) pour que l'intégrale de a à l'infini des f(x)dx CV est l = 0.

[Lostounet]

Certes il y a aussi des fonctions dont la limite en l'infini est nulle et dont l'intégrale de a à l'infini DV.
Mais ce que j'essaie de démontrer, c'est : lorsque f admet une limite l en l'infini , alors une condition nécessaire (non suffisante !) pour que l'intégrale de a à l'infini des f(x)dx CV est l = 0.

Je tente ma chance (à vérifier):


Soit f une fonction à valeurs positives admettant une limite L non nulle lorsque x tend vers . , et telle que l'intégrale sur converge.


Pour , nous obtenons un rang Y, tel que, pour tout
|f(x) - L| < L/2

donc: L - f(x) < L/2
Finalement,
En intégrant les deux membres sur , puis en faisant tendre b vers , nous contredisons l'hypothèse que l'intégrale converge (par minoration) dès que L est non nulle.

Conclusion: L est nécessairement nulle.

Autres choses à dire: il me semble que si tu enlèves l'hypothèse "admet une limite ", cela devient rapidement faux (vu qu'il y a des fonctions non bornées mais dont l'intégrale converge sur [a ; + infini[ (comme tu as du le voir certainement en cours avec la fonction "dents croissantes")
Et si tu retires cette hypothèse mais que tu rajoutes "f positive, uniformément continue" il me semble que cela implique que f est de limite nulle.

Si quelqu'un pouvait confirmer?

[Kolis]

Bonjour lostounet !
Effectivement si l'intégrale d'une fonction uniformément continue est convergente, la fonction a une limite nulle en .
Il suffit de raisonner par l'absurde en utilisant le critère de Cauchy.

A noter que la question initiale pourrait être remplacée par : si l'intégrale d'une fonction monotone est convergente, la fonction a une limite nulle.

[flashnext]

Merci pour la démo ! Juste une petite question : pourquoi ajoutes-tu l'hypothèse f "à valeurs positives" ?

effectivement il est nécessaire que f ait une limite. Tu veux que je poste un contre-exemple ?

[Lostounet]

Bonjour,

@Kolis: merci!

@flashnext: il me semble que les règles de majoration, de minoration (de comparaison et d'équivalents) ne s'appliquent que lorsqu'on manipule des fonctions positives (ou bien de signe constant au voisinage de b en s'adaptant).

Mais ici... la fonction L/2 est déjà du même signe que f au voisinage de l'infini... non?
Donc j'ai quelques doutes ici (dans l'attente de Kolis, Ben ou Doraki ...)

[Ben314]

Salut,
Tu n'a pas besoin de la positivité de vu que tout se passe "au voisinage de +oo" et que l'hypothèse disant que admet une limite L non nulle en +oo entraine que reste de signe constant sur un certain [b,+oo[ avec b>a

[Lostounet]

Je me disais aussi ! Merci Ben.

Par contre pour le cas uniformément continu, on en a besoin non?

[Ben314]

Non, pas plus (et heureusement !!!) :

Si est uniformément continue sur [a,+oo[, alors, pour 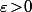fixé, il existe 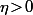tel que .
Donc, pour tout , on a :

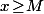Or, si est convergente, alors donc il existe tel que pour tout on ait et donc .

[flashnext]

Merci beaucoup ! À une prochaine et…
Joyeux Noël !