Systeme equations differentielles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
firefighter90
- Membre Naturel
- Messages: 42
- Enregistré le: 07 Nov 2014, 22:00
-
par firefighter90 » 15 Déc 2016, 16:42
Bonjour,
J'ai le système suivant avec les fonction
et
(
et
des constantes dans
):
}}{{\partial {t^2}}} = {k_1}\sqrt {{{\left( {\frac{{de}}{{dt}}} \right)}^2} + {{\left( {\frac{{dh}}{{dt}}} \right)}^2}} \times \left( {\frac{{de}}{{dt}}} \right)}\\ {\frac{{{\partial ^2}h(t)}}{{\partial {t^2}}} = {k_1}\sqrt {{{\left( {\frac{{de}}{{dt}}} \right)}^2} + {{\left( {\frac{{dh}}{{dt}}} \right)}^2}} \times \left( {\frac{{dh}}{{dt}}} \right) - {k_2}} \end{array}} \right.)
J'ai pensé à utiliser un changement de variable pour réduire l'ordre du système:
 = \frac{{de(t)}}{{dt}}}\\ {g(t) = \frac{{dh(t)}}{{dt}}}\\ {\frac{{df(t)}}{{dt}} = {k_1}\sqrt {{f^2} + {g^2}} \times f}\\ {\frac{{dg(t)}}{{dt}} = {k_1}\sqrt {{f^2} + {g^2}} \times g - {k_2}} \end{array}} \right.\])
Quelle méthode je peux utiliser pour la résolution analytique? Je sais déjà le faire numériquement mais pour mon application c'est utilisé tellement de fois que c'est trop coûteux!
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 15 Déc 2016, 18:32
Salut,
Vu la forme du bidule, y'a pas photo, il faut que tu passe en polaire en écrivant
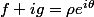
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
