Appliquer newton-raphson

[firefighter90]

bonjour,

J'ai une fonction qui dépend de deux variables et . Je cherche la solution tel que numériquement.

J'essaye d'appliquer la méthode de Newton-Raphson comme suit:

Je pose et je cherche à résoudre .

Le problème est que est non carrée: . Donc pour éviter de calculer l'inverse de , je pose et calcule plutôt . Ceci devrait donner qui permet de déduire , sauf que le développement donne une équation à deux inconnues: et donc pas de solution unique pour ?

Est-ce que j'ai faux ou bien l'algorithme n'est pas adapté, dans ce cas qu'elle autre méthode je peux creuser?
J'ajoute que ma fonction n'a pas d'expression analytique mais ça je peux le gérer par les différences finies!

merci

[Ben314]

Salut,
Je comprend pas trop ton truc : ta fonction f, certes, elle "dépend de deux variables x et y", mais le moins qu'on puisse dire, c'est que c'est on ne peu plus flou comme énoncé :
- les "variables" x et y, c'est quoi ? des réels ? , des complexes ?, des vecteurs ? des matrices ?, autre chose ?
- De même, le "résultat" de ta fonction, c'est quoi ?
Enfin, bref, lorsque l'on parle d'une "fonction" f il faut forcément écrire f:Ensemble_de_départ->Ensemble_d'arrivé pour que ça commence à être utilisable.

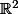
Là, en "lisant entre les lignes", ça donne vaguement l'impression que (ou éventuellement d'une partie de dans ). Sauf que dans ce cas, d'écrire comme tu le fait "je cherche la solution de f(x,y)=0" c'est totalement dénué de sens : les solutions de f(x,y)=0, ça s'apelle "la ligne de niveau de 0" et, pour la plupart des fonctions "assez simples" , c'est une courbe.
Par exemple, si (x,y)=coordonnées géographiques et f(x,y)=altitude, les solutions de f(x,y)=0, ben c'est les points à altitude 0, c'est à dire les "côtes" (= points au bord de la mer) et il y en a en général un sacré paquet.

Et dans un tel contexte de fonction , où E et F sont différents, on risque pas d'appliquer la méthode de Newton-Raphson sans (assez grosses) modifications. Par exemple ça :

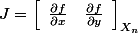
Le problème est que est non carrée: . Donc pour éviter de calculer l'inverse de

C'est une énorme monstruosité : une matrice non carré ne peut pas être inversible (c'est le B-A-BA du calcul matriciel) donc tu ne risque pas d'avoir à "éviter de calculer l'inverse".
Et tu t'en rend parfaitement compte 2 lignes dessous : le système que tu as à résoudre admet bien évidement une infinité de solutions (2 inconnues et une seule équation vu que ta matrice n'est pas carrée....)

Bon, sinon, il doit évidement y avoir moyen de "bricoler" la méthode pour que ça donne quelque chose, mais ça va pas te donner grand chose comme indication concernant l'ensemble des solutions de f(x,y)=0.
Par exemple, si f(x,y)=x²+y²-1, les solutions de f(x,y)=0, c'est le cercle trigo. et une "méthode bricolée", au mieux, elle te donnera comme "solution" un (et un seul) des points du cercle trigo ce qui va pas être super terrible comme info. On peut éventuellement dire que c'est mieux que rien, mais c'est quand même pas génial comme info de connaitre une unique solution parmi une énorme infinité.

[firefighter90]

Merci pour la réponse. Vous avez raison, il n'y a pas de solution unique bien évidement . Je me dirige donc vers un problème d'optimisation où l'objectif est de minimiser . Grâce à l'algo du Simplex et Matlab, ça se fait tout seul .

[Ben314]

Dans le contexte d'une fonction "un peu quelconque" de R²->R dont on cherche le minimum, ben je vois pas trop le rapport avec l'algo. du simplexe qui permet de minimiser/maximiser une fonction linéaire avec des contraintes linéaires.
Ici, ta fonction n'est (à priori) pas linéaire et en plus... tu as pas de contrainte... donc je vois vraiment pas le moindre rapport avec l'algo. du simplexe.

Par contre, si tu cherche à minimiser/maximiser f(x,y), là, tu pourrait éventuellement utiliser la méthode de Newton vu que tu cherche les points (x,y) où la matrice jacobienne est nulle et que l'application (x,y)->Jacobienne_en_(x,y), c'est bien du R²->R² (modulo les précautions d'usage lorsque l'on utilise cette méthode)

En plus, je comprend pas trop ton truc : pour moi, chercher les solution de f(x,y)=0 ou chercher les max/min de f(x,y), ça a quasiment rien à voir l'un avec l'autre, donc je comprend pas trop quel peut être ton contexte pour que tu décide de complètement changer ton fusil d'épaule.

[firefighter90]

juste pour info car j'ai déjà résolu mon problème:

le nom complet de l'algo c'est : "downhill simplex method" appelé aussi "Nelder–Mead method" qui marche pour de l'optimisation non linéaire sans contraintes. Dans mon problème je sais que et donc j'arrive à résoudre mon problème en ayant recours à un algo de minimisation.