Calcul de déterminant
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Hoog
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Sep 2006, 00:02
-
par Hoog » 13 Oct 2006, 01:33
Est-ce que quelqu'un pourrait m'aider à calculer det(M) sans trop souffrir dans les calculs (ça doit être faisable mais je ne vois pas trop les transfos) ?
Il paraît que le résultat peut s'écrire sous la forme mx+p (avec m et p fonctios des
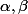
et
)
Merci aux courageux ! :we:
-
Hoog
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Sep 2006, 00:02
-
par Hoog » 13 Oct 2006, 01:33
Ah oui, M c'est la matrice bien sûr !
-
acb
- Membre Naturel
- Messages: 28
- Enregistré le: 07 Oct 2006, 18:14
-
par acb » 13 Oct 2006, 08:41
bonjour,
essaie de faire apparaitre des zéros dans les lignes ou colonnes pour pouvoir simplifier le calcul en faisant des combinaisons linéaires ou en colonnes. par ex, L2=L2-L3 etc.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 13 Oct 2006, 08:46
Retranche la dernière colonne à toutes les autres :
Si on développe ensuite le determinant suivant la dernière colonne on voit bien qu'il va avoir la forme que tu dis :
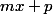
. Reste à trouver
et
.
Pour cela on remarque que si
=\begin{bmatrix} a_1-x & \beta-x & \beta-x & \cdots & \beta-x \\ \alpha-x & a_2-x & \beta-x & \cdots & \beta-x \\ \alpha-x & \alpha-x & a_3-x & \cdots & \beta-x \\ \vdots & & \ddots & & \vdots \\ \alpha-x & \alpha-x & \alpha-x & \cdots & a_n-x\end{bmatrix})
alors
)
est une matrice triangulaire supérieure dont le déterminant est le produit des elements diagonaux :
)
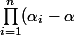donc
)
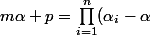De même avec
)=\prod_{i=1}^{n}(\alpha_i-\beta)=m\beta+p)
On en deduit assez facilement
et
...
-
Hoog
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Sep 2006, 00:02
-
par Hoog » 14 Oct 2006, 12:33
Merci Tize, je viens seulement de reprendre ça ... et ça marche ! :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
