Fonction dérivée

[Lalo]

Bonjour,

J'ai un problème pour résoudre cet exercice, pourriez-vous m'aider ?

Déterminer le taux d'accroissement de la fonction f définie sur R par f(x) = .
En déduire le nombre dérivé de f en -2.

Merci

[Ben314]

Salut,
C'est quoi le "taux d'accroissement d'une fonction" ?

[Lalo]

C'est le nombre

Il rentre en compte dans les nombres et fonctions dérivés mais je ne sais pas comment t'expliquer davantage à quoi il correspond.

[Ben314]

Ben déjà, écrit ce que ça donne dans le cas de la fonction f que l'on t'a donné.
Et je pense aussi qu'il faut prendre a=2 (i.e. calculer le taux d'accroissement au point 2) vu la question suivante, mais c'est pas complètement évident : fait comme tu veut...

Ensuite, c'est effectivement ce taux d'accroissement qui permet de définir le nombre dérivé d'une fonction au point a (ici a=2) : c'est la limite du taux d'accroissement lorsque h tend vers 0.

[Lalo]

J'ai utilisé la formule du taux d'accroissement avec les valeurs :

f(-2) =

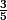
f(-2 + h) =

mais mon résultat final ne me semble pas juste

[Lalo]

Je pense que mon erreur vient du développement de l'expression :


=
= ...

[Ben314]

Jusque là, c'est bon.
Reste la partie "calculs" (réduction au même dénominateur, etc...)

[Lalo]

Après avoir repéré une erreur et modifié mon développement, voici mon expression finale :


Est-ce le taux d'accroissement ? Je pensais pouvoir réduire encore cette expression

[Ben314]

Oui, c'est bon.
Et c'est suffisamment simplifié pour permettre de voir immédiatement vers quoi tend cette quantité lorsque h tend vers 0.
Le truc qui posait problème dans l'expression de départ c'est la division par h qui faisait qu'on ne pouvait pas prendre h=0 et que, pour h "proche de 0", le numérateur et le dénominateur étaient quasiment nuls donc qu'on ne pouvait pas trop savoir la valeur du quotient.
Bref, le but du jeu, c'est principalement d'éliminer le h du dénominateur et là, c'est O.K.

[Lalo]

Très bien, merci de m'avoir aidée !

Bonne soirée