Bonjour, je rencontre un soucis pour résoudre une suite arithmétique:
Elle est de la forme "un+1 = (-60 + un ) - (n * 78)
U0 = -102
Le but est de calculé U10
J'arrive à calculer U10, mais en calculant successivement les valeurs de u1, u2, u3... jusqu'à u10!
J'ai par exemple (pour u1):
u1 = (-60 -102 ) - (0 * 78)
u1 = -162
u2 = (-60 -162) - (1 * 78)
u2 = -222 - 78
u2 = -300
...
Je sais que par définition
Un = U0 + nr --> mais là vu que la raison ne semble jamais là même, ça n'est pas applicable?
Ma super vraie question: comment arriver à calculer directement u10?
Suite arithmétique problème de compréhension
4 messages
- Page 1 sur 1
Re: suite arithmétique problème de compréhension
bonjour
pas de moyen direct...
comme tu l'as fait remarquer ce n'est pas une suite arithmetique!
le seul moyen que je vois est de calculer u(n) en fonction de n
u(n) = u(n-1) -60 - 78*(n-1)
u(n-1) = u(n-2) -60 - 78(n-2)
.....
u2 = u1 -60 -78*1
u1 = u0 -60
et en additionnant toutes les equations et en simplifiant on obtient (sauf erreur)
u(n) = u0 - 60*n -78*( 1+2+3+...+n-1)
u(n) = .......
pas de moyen direct...
comme tu l'as fait remarquer ce n'est pas une suite arithmetique!
le seul moyen que je vois est de calculer u(n) en fonction de n
u(n) = u(n-1) -60 - 78*(n-1)
u(n-1) = u(n-2) -60 - 78(n-2)
.....
u2 = u1 -60 -78*1
u1 = u0 -60
et en additionnant toutes les equations et en simplifiant on obtient (sauf erreur)
u(n) = u0 - 60*n -78*( 1+2+3+...+n-1)
u(n) = .......
Re: suite arithmétique problème de compréhension
Salut Jeffrey !
Une autre manière de trouver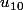 sans faire trop de calculs.
sans faire trop de calculs.
De ta relation , on a l'égalité
, on a l'égalité ) :
:  .
.
En prenant les égalités) pour
pour  allant de
allant de  jusqu'à
jusqu'à  , et en les sommant membre à membre, on a :
, et en les sommant membre à membre, on a :
 = \sum_{n=0}^9 (-78n -60))
où de façon générale, si on a une suite de réels) ,
,  (autrement, c'est la somme des termes de la suite d'indices consécutifs où l'on commence à sommer à partir de
(autrement, c'est la somme des termes de la suite d'indices consécutifs où l'on commence à sommer à partir de  et on s'arrête à
et on s'arrête à  ).
).
En remarquant que :
=(u_{10}-u_9)+( u_9-u_8)+(u_8-u_7)+( u_7-u_6)+...+( u_2-u_1)+( u_1-u_0)=u_{10}-u_0) ,
,
(presque tous les termes se compensent) on en déduit que) .
.
Reste alors à calculer) . Soit on utilise des propriétés du symbole d'addition
. Soit on utilise des propriétés du symbole d'addition  , soit on revient à une écriture avec des
, soit on revient à une écriture avec des 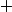 . Dans les deux cas, on a :
. Dans les deux cas, on a :
 = \sum_{n=0}^9 (-78n) + \sum_{n=0}^9 ( -60) = -78 \sum_{n=0}^9 n -60 \sum_{n=0}^9 1)
Il faut donc connaître la somme de entiers consécutifs (il y a dix entiers entre
entiers consécutifs (il y a dix entiers entre  et
et  ) en comptant à partir de
) en comptant à partir de  (la somme commence à
(la somme commence à  ). Ca peut se calculer à la main. Sinon, on utilise l'égalité suivante :
). Ca peut se calculer à la main. Sinon, on utilise l'égalité suivante :
}{2})
Dans le cas où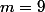 , on a que
, on a que }{2}=45) . Dans la somme
. Dans la somme  , on additionne
, on additionne  fois (il y a
fois (il y a  entier entre
entier entre  et
et  ) le nombre
) le nombre  donc
donc  .
.
En conclusion, , donc par conséquent :
, donc par conséquent :

Une autre manière de trouver
De ta relation
En prenant les égalités
où de façon générale, si on a une suite de réels
En remarquant que :
(presque tous les termes se compensent) on en déduit que
Reste alors à calculer
Il faut donc connaître la somme de
Dans le cas où
En conclusion,
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
